Tìm giá trị của m để đa thức ( x3 + 3x2 - 5x + m ) chia hết cho ( x - 2 )
Giải bởi qa.haylamdo.com
Tìm giá trị của m để đa thức ( x3 + 3x2 - 5x + m ) chia hết cho ( x - 2 )
Hướng dẫn giải:
Nhận xét: Ở đây, ta có thể đặt phép chia của ( x3 + 3x2 - 5x + m ) cho ( x - 2 ) để tìm số dư, rồi cho số dư đó bằng 0, từ đó tìm được giá trị của m.
Mở rộng: Bài toán này ta áp dụng phân tích đa thức thành nhân tử để giải toán.
Ta có: ( x3 + 3x2 - 5x + m ) = ( x3 - 2x2 ) + ( 5x - 10 ) + m + 10
= x2( x - 2 ) + 5( x - 2 ) + m + 10
Nhận thấy:
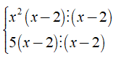
Khi đó để ( x3 + 3x2 - 5x + m ) cho ( x - 2 ) khi và chỉ khi m + 10 = 0 ⇔ m = - 10.
Vậy m = - 10 là giá trị cần tìm.
Rút gọn biểu thức xn( xn + 1 + yn ) - yn( xn + yn - 1 ) được kết quả là?
Chứng tỏ rằng các biểu thức sau không phụ thuộc vào biến x
a, x( 2x + 1 ) - x2( x + 2 ) + ( x3 - x + 3 )
Thực hiện phép tính ( 5x - 1 )( x + 3 ) - ( x - 2 )( 5x - 4 ) ta có kết quả là ?
Giá trị nhỏ nhất của biểu thức 9x2 - 6x + 5 đạt được khi x bằng ?
Tính giá trị của biểu thức sau A = x6 - 2x4 + x3 + x2 - x, biết x3 - x = 6.
Tính giá trị của các biểu thức sau
a, P = 12x4y2:( - 9xy2 ) tại x = - 3;y = 1,005.
