Cho tứ giác ABCD có = 700, = 900. Các tia phân giác của các góc C và D cắt nhau tại O. Tính số đo góc CODˆ ?
Giải bởi qa.haylamdo.com
Áp dụng định lí: Tổng các góc của một tứ giác bằng 3600.
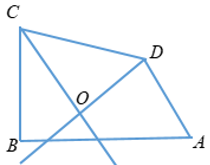
Ta có = 3600 ⇒ = 3600 - ( ) = 3600 - ( 700 + 900 )
⇒ = 2000
Theo giả thiết, ta có OC, OD là các đường phân giác
Khi đó ta có
⇒ = =
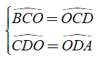
⇔ 2() = 2000 ⇔ = 1000
Xét Δ OCD có = 1800 ⇒ = 1800 - () = 1800 - 1000 = 800.
Vậy = 800.
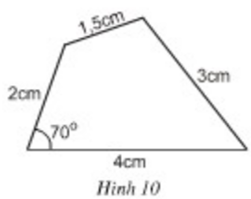
Ta gọi tứ giác ABCD trên hình 8 có AB = AD, CB = CD là hình "cái diều". Tính ∠B, ∠D biết rằng ∠A= 1000 và ∠C= 600 .
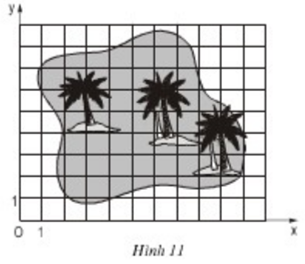
Đố em tìm thấy vị trí của "kho báu" trên hình 11, biết rằng kho báu nằm tại giao điểm các đường chéo của tứ giác ABCD, trong đó các đỉnh của tứ giác có tọa độ như sau: A(3; 2), B(2; 7), C(6; 8), D(8; 5).
Tính tổng các góc ngoài của tứ giác ở hình 7b ( tại mỗi đỉnh của tứ giác chỉ chọn một góc ngoài):
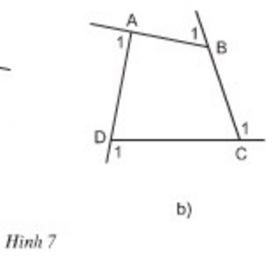
Góc kề bù với một góc của tứ giác gọi là góc ngoài của tứ giác.
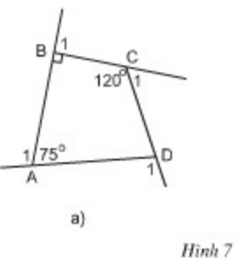
Tính các góc ngoài của tứ giác ở hình 7a.
Cho tứ giác ABCD trong đó = 730, = 1120, = 840. Tính số đo góc ?
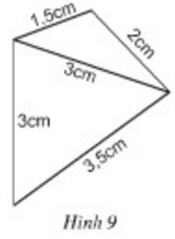
Dựa vào cách vẽ các tam giác đã học, hãy vẽ lại các tứ giác ở hình 9 vào vở.
