Cho AB/A'B' = CD/C'D'

⇔ AB.C'D' = A'B'.CD    ( I )

⇔ AB/CD = A'B'/C'D'    ( II )

Cho tam giác ABC vuông tại A, đường cao AH có AB = 15cm;AC = 20cm. Tia phân giác của góc HAB cắt HB tại D, tia phân giác của góc HAC cắt HC tại E. Tính độ dài các đoạn AH, HD và HE.

Cho đoạn thẳng AB = 10 cm

a) Trên đoạn thẳng AB lấy điểm C sao cho CA/CB = 3/2 . Tính độ dài đoạn CB.

b) Trên tia đối của tia BA lấy điểm D sao cho DA/DB = 3/2 . Tính độ dài đoạn CD.

Cho tam giác ABC có BC = a; CA = b; AB = c. Các đường phân giác AD, BE, CF cắt nhau tại I. Chứng minh rằng:

$a) \frac{DI}{DA}=\frac{a}{a+b+c}$

$b) \frac{DI}{DA}+\frac{EI}{EB}+\frac{FI}{FC}=1$

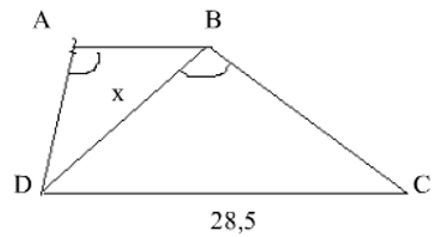
Cho hình bên, ABCD là hình thang ( AB//CD ) có AB = 12,5cm; CD = 28,5cm; DABˆ = DBCˆ . Tính độ dài đoạn BD gần nhất bằng bao nhiêu?

Cho hình bên. Chọn câu trả lời đúng?

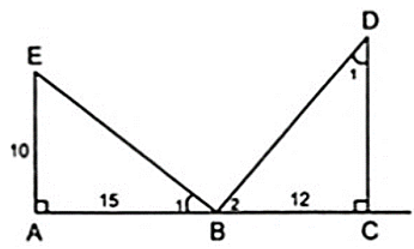
Cho hình vẽ như bên, biết EBAˆ = BDCˆ

a) Trong hình vẽ có bao nhiêu tam giác vuông? Kể tên các tam giác vuông đó.

b) Cho AE = 10cm, AB = 15cm, BC = 12cm. Hãy tính độ dài các đoạn thẳng CD, BE, BD và ED (làm tròn đến chữ số thập phân thứ nhất)

c) So sánh diện tích tam giác BDE với tổng diện tích hai tam giác AEB và BCD