Cho hình thang ABCD . Một đường thẳng song song với hai đáy, cắt các cạnh bên AD và BC theo thứ tự ở M và N.Chứng minh rằng:
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
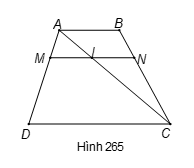
Gọi I là giao điểm của đường chéo AC với MN.
Áp dụng định lí Ta-lét vào hai tam giác ACD và ACB
có , ta được:
(1); (2).
Từ (1) và (2) suy ra: .
Cho hình thang . Một đường thẳng song song với hai đáy, cắt các cạnh bên AD và BC theo thứ tự ở M và N. Chứng minh rằng: