Cho hình thang ABCD và điểm E trên cạnh bên BC. Qua C vẽ đường thẳng song song với AE cắt AD ở K. Chứng minh rằng BK//DE.

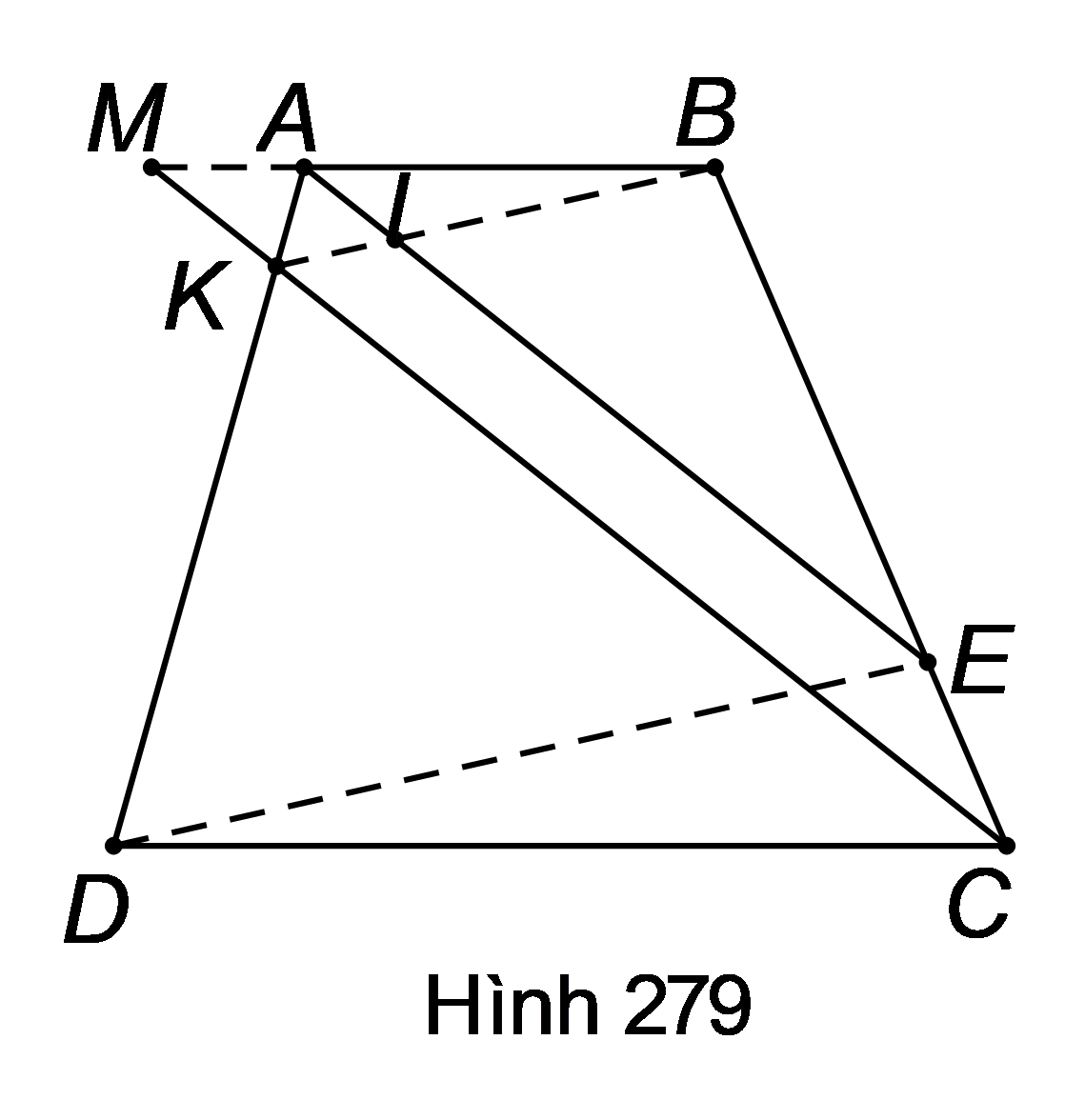
Gọi I,M lần lượt là giao điểm của AE với BK và CK với AB.

Áp dụng hệ quả của định lí Ta-lét cho $AI\parallel MK$  và $IE\parallel KC$ , thu được:

           $\left\{\begin{array}{c}\frac{AI}{MK}=\frac{BI}{BK}\\ \frac{BI}{BK}=\frac{IE}{KC}\end{array}\right.\Rightarrow \frac{AI}{MK}=\frac{IE}{KC}\Rightarrow \frac{AI}{IE}=\frac{MK}{KC}$  (1).

Áp dụng hệ quả của định lí Ta-lét cho $MA\parallel DC$ , ta được:

             $\frac{MK}{KC}=\frac{AK}{KD}$(2).

Từ (1) và (2) suy ra $\frac{AI}{IE}=\frac{AK}{KD}$ . Điều này chứng tỏ đường thẳng KI cắt hai cạnh $AD,AE$  của tam giác ADE và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ nên $KI\parallel DE$ , hay $KB\parallel DE$  (theo định lí Ta-lét đảo).