Cho hình thang cân ABCD (AB // CD) có AB = 3, BC = CD = 13 (cm). Kẻ các đường cao AK và BH.
a) Chứng minh rằng CH = DK.
Giải bởi qa.haylamdo.com
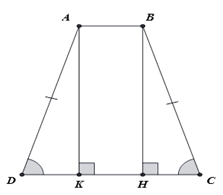
a) và có cạnh huyền BC = AD (cạnh bên hình thang cân), góc nhọn (góc đáy hình thang cân).
Do đó (cạnh huyền, góc nhon), suy ra CH = DK.
Cho hình thang ABCD cân có AB // CD và AB < CD. Kẻ các đường cao AE, BF.
a. Chứng minh rằng: DE = CF.
Cho hình thang cân ABCD (AB//CD, AB < CD). AD cắt BC tại O.
a) Chứng minh rằng OAB cân
c. Tia DA và tia CB cắt nhau tại O. Chứng minh OI vừa là trung trực của AB vừa là trung trực của DC.
c) Qua điểm M thuộc cạnh AC, vẽ đường thẳng song song với CD, cắt BD tại N. Chứng minh rằng MNAB, MNDC là các hình thang cân.
b. Gọi I là giao điểm của 2 đường chéo hình thang ABCD. Chứng minh: IA = IB.
