Giải bởi qa.haylamdo.com
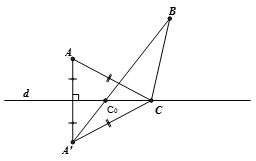
Gọi A’ là điểm đối xứng của điểm A qua đường thẳng d. Với mỗi điểm C trên đường thẳng d, ta có CA = CA'. Do đó: .
CA + CB nhỏ nhất khi CA' + CB = AB , hay C thuộc đoạn A'B. Vậy điểm C thỏa đề bài là giao điểm của đoạn BA’ với đường thẳng d.Cho tam giác ABC có , B và C là các góc nhọn. M là một điểm thuộc cạnh BC. Gọi D là điểm đối xứng với M qua AB, E là điểm đỗi ứng với M qua AC. Gọi I, K là giao điểm của DE với AB, AC.
a) Tính các góc của tam giác ADE.
Cho tam giác nhọn ABC, trực tâm H. Gọi K là điểm đối xứng với H qua BC. Tìm hệ thức liên hệ giữa số đo các góc BAC, BKC.
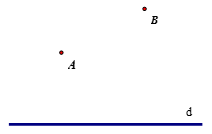
Cho đường thẳng d và hai điểm A, B (như hình vẽ). Tìm vị trí điểm C trên d để chu vi tam giác ABC nhỏ nhất.
Cho tam giác ABC vuông ở A, lấy D là điểm bất kì thuộc cạnh BC. Gọi E là điểm đối xứng với D qua AB, F là điểm đối xứng với D qua AC.
a) Chứng minh rằng A là trung điểm của EF.
Cho vuông tại A. Lấy M bất kì trên cạnh BC. Gọi E, F lần lượt là các điểm đối xứng với M qua AB, AC. Chứng minh A là trung điểm của EF.
Cho hình thang vuông . Gọi K là điểm đối xứng với C qua AD. CMR: .
Cho tam giác ABC có các đường phân giác BD, CE cắt nhau ở O. Qua A vẽ các đường vuông góc với BD và với CE, chúng cắt BC theo thứ tự ở N và M. Gọi H là chân đường vuông góc kẻ từ O đến BC. Chứng minh rằng:
a) M đối xứng với A qua CE, N đối xứng với A qua BD;
Cho tam giác ABC vuông tại A, đường cao AH. Gọi D và E lần lượt là điểm đối xứng của điểm H qua AB và AC. Chứng minh rằng:
a) A là trung điểm của đoạn DE
