Dạng 5. Phiếu bài tập tự luyện có đáp án
-
641 lượt thi
-
23 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
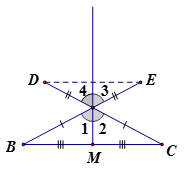
Chứng minh nên và AM là đường trung trực của DE
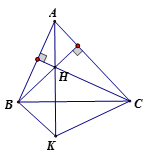
Câu 2:
Chứng minh B đối xứng với C qua AM
A đối xứng với A qua AM
=> đpcm.
Câu 3:
Cho tam giác nhọn ABC, trực tâm H. Gọi K là điểm đối xứng với H qua BC. Tìm hệ thức liên hệ giữa số đo các góc BAC, BKC.
Ta lại có nên
Câu 4:
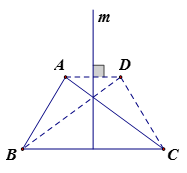
DC đối xứng với AB qua m, DB đối xứng với AC qua m
Câu 5:
a) Tứ giác ABCD là hình thang có hai đường chéo bằng nhau nên là hình thang cân.
Câu 7:
Cho , gọi d là đường phân giác ngoài ở đỉnh A. Trên đường thẳng d lấy điểm . CMR: .
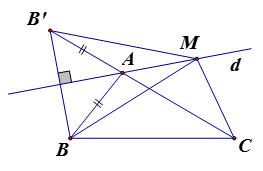
Trên tia đối của tia AC lấy điểm B' sao cho AB' = AB.
Dễ thấy B' đối xứng với B qua d, do B'M = BM
Câu 8:
Cho vuông tại A. Lấy M bất kì trên cạnh BC. Gọi E, F lần lượt là các điểm đối xứng với M qua AB, AC. Chứng minh A là trung điểm của EF.
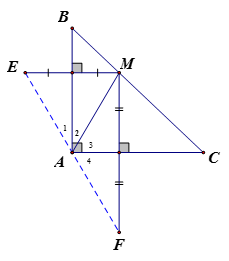
Sử dụng tính chất đối xứng trục
=> AE = AF (=AM) (1)
Sử dụng tính chất của tam giác cân
Từ đó chỉ ra được thẳng hàng (2)
(1)(2) => đpcm.
Câu 9:
Cho tam giác ABC cân tại B
a) Tìm trục đối xứng của tam giác đó
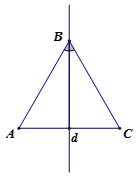
Câu 10:
a) Hình đối xứng qua d của đỉnh A là C, của đỉnh B là B, của đỉnh C là A, của cạnh AB là cạnh CB, của cạnh AC là AC.
Câu 11:
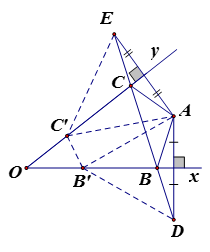
* Cách dựng:
- Dựng D đối xứng với A qua Ox
- Dựng E đối xứng với A qua Oy
- Ox, Oy cắt DE tại B và C.
* Chứng minh:
Gọi B’, C’ là các điểm bất kì thuộc Ox, Oy. Ta có:
(1)
(2)
Do nên chu vi chu viCâu 12:
Cho đường thẳng d và hai điểm A, B (như hình vẽ). Tìm vị trí điểm C trên d để chu vi tam giác ABC nhỏ nhất.
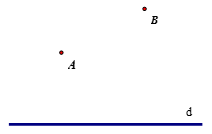
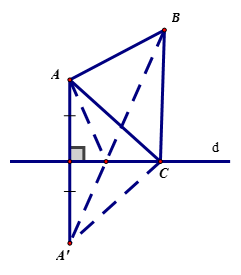
Gọi A' là điểm đối xứng của A qua d
=> A' cố định.
Vì (tc đối xứng trục)
Ta có:
(không đổi).
Dấu “=” xảy ra tức chu vi tam giác nhỏ nhất khi C là giao điểm của d và BA'
Câu 13:
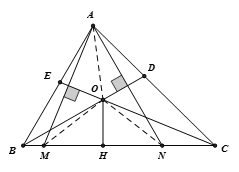
Cho tam giác ABC có các đường phân giác BD, CE cắt nhau ở O. Qua A vẽ các đường vuông góc với BD và với CE, chúng cắt BC theo thứ tự ở N và M. Gọi H là chân đường vuông góc kẻ từ O đến BC. Chứng minh rằng:
a) M đối xứng với A qua CE, N đối xứng với A qua BD;
Câu 14:
Câu 15:
Cho tam giác ABC vuông ở A, lấy D là điểm bất kì thuộc cạnh BC. Gọi E là điểm đối xứng với D qua AB, F là điểm đối xứng với D qua AC.
a) Chứng minh rằng A là trung điểm của EF.
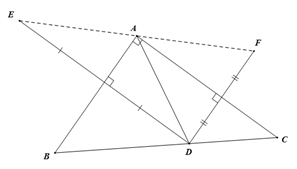
a) E là điểm đối xứng với AB qua AB
=> AF = AD là điểm đối xứng với D qua AB
Từ (1) và (3) suy ra .
Từ (2) và (4) suy ra
do đó nên A, E, F thẳng hàng (6)
Từ (5) và (6) suy ra A là trung điểm của EF,
Câu 16:
b) Ta có EF = 2AD nên: EF nhỏ nhất <=> AD nhỏ nhất <=> D là chân đường cao kẻ từ A đến BC.
Câu 17:
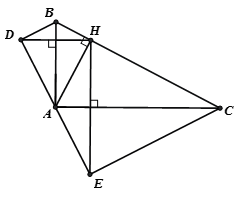
Cho tam giác ABC vuông tại A, đường cao AH. Gọi D và E lần lượt là điểm đối xứng của điểm H qua AB và AC. Chứng minh rằng:
a) A là trung điểm của đoạn DE
Câu 18:
b) Tứ giác BDEC là hình thang vuông.
b) Chỉ ra
Từ đó suy ra DB // EC => DBCE là hình thang có , do vậy BDEC là hình thang vuông tại D và E.
Câu 19:
c) BH = 2cm, CH = 8cm.
Trong tam giác ABH vuông tại H, theo định lý Pitago:
Trong tam giác ACH vuông tại H, theo định lý Pitago
Suy ra:
Lại có , suy ra
Vậy AH = 4
Đặt ![]() là chu vi hình thang BDEC.
là chu vi hình thang BDEC.
Ta có . Do đó:
Câu 20:
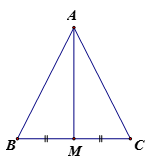
Cho tam giác ABC có , B và C là các góc nhọn. M là một điểm thuộc cạnh BC. Gọi D là điểm đối xứng với M qua AB, E là điểm đỗi ứng với M qua AC. Gọi I, K là giao điểm của DE với AB, AC.
a) Tính các góc của tam giác ADE.
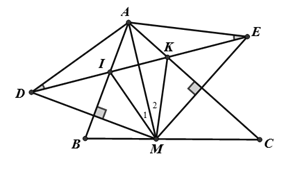
a) Tam giác ADE cân tại A,
Câu 22:
c) Điểm M ở vị trí nào trên cạnh BC thì DE có độ dài ngắn nhất?
c) Các tam giác ADE cân tại A, có góc ở đỉnh không đổi nên cạnh đáy DE nhỏ nhất <=> cạnh bên AD nhỏ nhất <=> AM nhỏ nhất <=> M là chân đường vuông góc kẻ từ A đến BC(Do nhọn nên chân đường vuông góc đó nằm trên cạnh BC).
Câu 23:
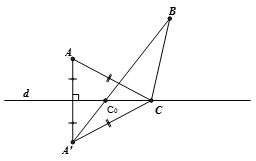
Gọi A’ là điểm đối xứng của điểm A qua đường thẳng d. Với mỗi điểm C trên đường thẳng d, ta có CA = CA'. Do đó: .
CA + CB nhỏ nhất khi CA' + CB = AB , hay C thuộc đoạn A'B. Vậy điểm C thỏa đề bài là giao điểm của đoạn BA’ với đường thẳng d.