Cho A và B là hai điểm thuộc cùng một nửa mặt phẳng có bờ là đường thẳng xy (AB không vuông góc với xy). Gọi A’ là điểm đối xứng với A qua xy, C là giao điểm của A’B và xy. Gọi M là điểm bất kỳ khác C thuộc đường thẳng xy.
Chứng minh rằng: AC + CB < AM + MB.
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
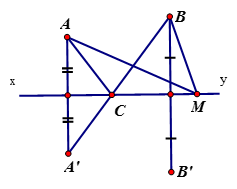
A’ đối xứng với A qua xy
=> xy là đường trung trực của AA’
và AC = A’C, AM = A’M
Ta có: AC + CB = A’C + CB = A’B (1)
AM + MB = A’M + MB (2)
Trong có: A’B < A’M + MB (quan hệ giữa 3 cạnh trong tam giác) (3)
Từ (1), (2), (3) suy ra: AC + CB < AM + MB.
Cho tam giác ABC. Gọi D là điểm đối xứng với A qua C, E là điểm đối xứng với B qua A, F là điểm đối xứng với C qua B. Gọi BM là trung tuyến của tam giác ABC, EK là trung tuyến của tam giác DEF.
a) Chứng minh rằng ABKM là hình bình hành.
Cho tam giác ABC vuông tại A ( AB < AC), điểm D thuộc cạnh huyền BC. Vẽ điểm M và điểm N đối xứng với D lần lượt qua AB và AC. Chứng minh rằng:
a) M và N đối xứng qua A.
Cho hình bình hành ABCD. Vẽ E là điểm đối xứng của A qua B, F là điểm đối xứng của A qua D. Chứng minh rằng: E là điểm đối xứng của F qua C.
Cho hình bình hành ABCD, điểm P trên AB. Gọi M, N là các trung điểm của AD, BC; E, F lần lượt là điểm đối xứng của P qua M, N. Chứng minh rằng:
a) E, F thuộc đường thẳng CD.b) Tam giác ABC phải có thêm điều kiện gi để điểm E đối xứng với điểm F qua điểm A.
b) Gọi G là giao điểm của BM và EK. Chứng minh rằng G là trọng tâm của hai tam giác ABC và tam giác DEF.
Cho tam giác ABC, D là một điểm trên cạnh BC. Gọi E và F theo thứ tự là điểm đối xứng của điểm D qua AB và AC.
a) Chứng minh AE = AF;