Dạng 4: Bài nâng cao phát triển tư duy có đáp án
-
608 lượt thi
-
14 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
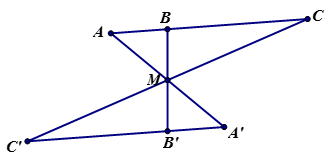
Giả sử A, B, C thẳng hàng theo thứ tự đó, ta có AB + BC = AC (1).
Các đoạn thẳng A’B’, B’C’ và A’C’ lần lượt đối xứng với các đoạn thẳng AB, BC, AC qua điểm M nên ta có A’B’ = AB, B’C’ = BC, A’C’ = AC.
Kết hợp đẳng thức (1) ta được A’B’ + B’C’ = A’C’. Vậy A’, B’, C’ thẳng hàng.
Câu 2:
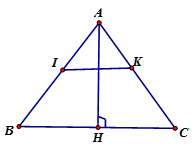
Vì ABC cân tại A, AH là đường cao nên AH là tia phân giác của góc A
Lại có: IA = AK => IAK cân tại A, mà AH là tia phân giác của góc A (cmt) => AH là đường trung trực của IK => Điểm I đối xứng với điểm K qua AH
Câu 3:
Cho hình bình hành ABCD. Vẽ E là điểm đối xứng của A qua B, F là điểm đối xứng của A qua D. Chứng minh rằng: E là điểm đối xứng của F qua C.
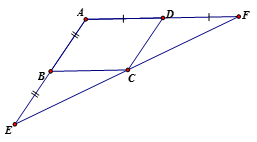
E là điểm đối xứng của A qua B (gt) nên AB = BE
Tứ giác ABCD là HBH =>
Mà AB = BE (cmt) => Tứ giác BDCE là hình bình hành
=> BD // EC và BD = EC.
Chứng minh tương tự cũng có BD // CF và BD = CF.
Vì BD // EC và BD // CF => E, C, F thẳng hàng (tiên đề Ơ-clit) Mà EC = CF (= BD) nên C là trung điểm EF => E là điểm đối xứng của F qua C.
Câu 4:
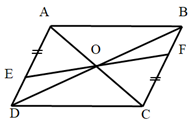
Gọi O là giao điểm cuả AC, BD.
Tứ giác ABCD là hình bình hành(gt) => O là trung điểm của AC
Tứ giác AECF có AE = CF, AE // CF nên là hình bình hành (dhnb)
mà O là trung điểm AC nên O là trung điểm EF.
=> EF đi qua O. Vậy các đường thẳng AC, BD, EF đồng quy tại điểm O.
Câu 5:
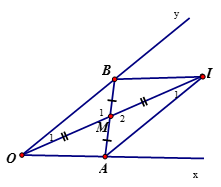
Cách dựng:
- Dựng điểm I đối xứng với O qua điểm M.
- Qua I dựng đường thẳng song song với Oy cắt Ox ở A.
- Dựng đường thẳng AM cắt Oy ở B.
Chứng minh:
Xét và có:
( hai góc so le trong)
MO = MI ( Vì I và O đối xứng nhau qua M)
( hai góc đối đỉnh)
=> (g.c.g) => MA = MB ( 2 cạnh tương ứng)
Bài toán luôn luôn dựng được một và có một nghiệm hình.
Câu 6:
Cho hình bình hành ABCD, điểm P trên AB. Gọi M, N là các trung điểm của AD, BC; E, F lần lượt là điểm đối xứng của P qua M, N. Chứng minh rằng:
a) E, F thuộc đường thẳng CD.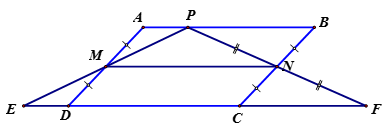
a) M là trung điểm của AD và PE suy ra tứ giác APDE là hình bình hành => DE // AP.
N là trung điểm của BC và PF suy ra tứ giác BPCF là hình bình hành => FC // PB.
Mặt khác CD // AB nên suy ra các điểm E, F nằm trên đường thẳng CD.
Câu 8:
Cho tam giác ABC, D là một điểm trên cạnh BC. Gọi E và F theo thứ tự là điểm đối xứng của điểm D qua AB và AC.
a) Chứng minh AE = AF;
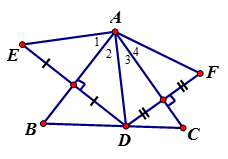
a) E đối xứng với D qua AB => AB là trung trực của ED => AE = AD.
F đối xứng với D qua AC => AC là trung trực của DE => AF = AD.
=> AE = AF.
Xét cân tại A, có AB là trung trực => AB đồng thời là phân giác của
=>
Xét cân tại A, có AC là trung trực => AC đồng thời là phân giác của
=>
=>
Câu 9:
b) Tam giác ABC phải có thêm điều kiện gi để điểm E đối xứng với điểm F qua điểm A.
b) Để E đối xứng với F qua A thì E, A, F thẳng hàng.
Vậy nếu vuông ở A thì E đối xứng với F qua điểm A.
Câu 10:
Cho tam giác ABC. Gọi D là điểm đối xứng với A qua C, E là điểm đối xứng với B qua A, F là điểm đối xứng với C qua B. Gọi BM là trung tuyến của tam giác ABC, EK là trung tuyến của tam giác DEF.
a) Chứng minh rằng ABKM là hình bình hành.
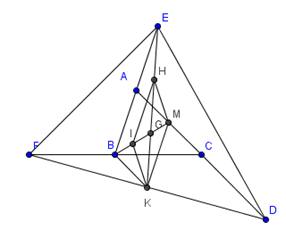
a) BK là đường trung bình của tam giác CFD. Suy ra BK//CD,
Mà CD = CA, => BK // AM, BK = AM
Suy ra tứ giác ABKM là hình bình hành
Câu 11:
b) Gọi G là giao điểm của BM và EK. Chứng minh rằng G là trọng tâm của hai tam giác ABC và tam giác DEF.
b) Gọi G là giao điểm của EK, BM. I, H là trung điểm của BG, EG.
- Chứng minh tứ giác HMKI là hình bình hành:
Ta có: H là trung điểm của GE (gt)
I là trung điểm của GB (gt)
=> HI là đường trung bình của (1)
+) Tứ giác ABKM là hình bình hành ( cm câu a)
Mà E đối xứng với B qua A => A là trung điểm của BE
(2)
Từ (1) và (2) => tứ giác HMKI là hình bình hành
- Suy ra GH = GK, GI = GM, từ đó ta có => G là trọng tâm tam giác DEF cũng là trọng tâm tam giác ABC.
Câu 12:
Cho A và B là hai điểm thuộc cùng một nửa mặt phẳng có bờ là đường thẳng xy (AB không vuông góc với xy). Gọi A’ là điểm đối xứng với A qua xy, C là giao điểm của A’B và xy. Gọi M là điểm bất kỳ khác C thuộc đường thẳng xy.
Chứng minh rằng: AC + CB < AM + MB.
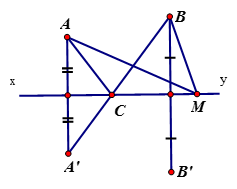
A’ đối xứng với A qua xy
=> xy là đường trung trực của AA’
và AC = A’C, AM = A’M
Ta có: AC + CB = A’C + CB = A’B (1)
AM + MB = A’M + MB (2)
Trong có: A’B < A’M + MB (quan hệ giữa 3 cạnh trong tam giác) (3)
Từ (1), (2), (3) suy ra: AC + CB < AM + MB.
Câu 13:
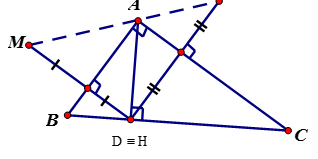
Cho tam giác ABC vuông tại A ( AB < AC), điểm D thuộc cạnh huyền BC. Vẽ điểm M và điểm N đối xứng với D lần lượt qua AB và AC. Chứng minh rằng:
a) M và N đối xứng qua A.
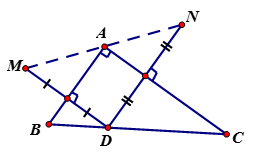
a) AM đối xứng với AD qua AB nên (1)
AN đối đối xứng với AD qua AC nên (2)
Từ (1) và (2) và
=> 3 điểm M, A, N thẳng hàng
=> Mà AM = AN => M và N đối xứng qua A và MN = 2 AD.
Câu 14:
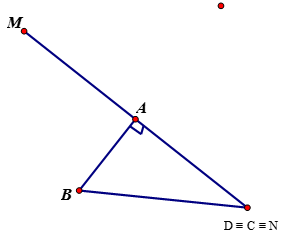
b) Vẽ , ta có
Vậy MN ngắn nhất bằng AH khi ( hình a)
Dựa vào quan hệ giữa đường xiên và hình chiếu , ta có
Do đó MN dài nhất bằng 2AC khi ( hình b)