Cho tam giác ABC nhọn, các đường cao AD, BE, CF đồng quy tại H. Gọi M, N, P, Q lần lượt là hình chiếu của D trên AB, BE, CF, CA. Chứng minh rằng M, N, P, Q thẳng hàng.
Giải bởi qa.haylamdo.com
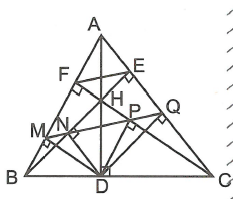
Vì (cùng vuông góc với AC) nên (định lý Ta-lét) (1).
Vì (cùng vuông góc với AB) nên (định lý Ta-lét) (2).
Từ (1) và (2) ta có (định lý Ta-lét đảo) (*).
Tương tự có (**)
Từ (*) và (**) có MN, MQ, PQ trùng nhau hay M, N, P, Q thẳng hàng. Vậy M, N, P, Q thẳng hàng
Qua giao điểm O của hai đường chéo tứ giác ABCD, kẻ một đường thẳng tùy ý cắt cạnh AB tại M, CD tại N. Đường thẳng qua M song song với CD cắt AC ở E và đường thẳng qua N song song với AB cắt BD ở F. Chứng minh BE//CF.
Cho tứ giác ABCD, vẽ các đường thẳng , song song với AC; cắt AD, DC theo thứ tự tại E và F; cắt AB, BC theo thứ tự tại G và H (G, H khác E, F). Chứng minh rằng EG, DB, HF đồng quy.
