Cho đoạn thẳng AB, điểm M chuyển động trên đoạn thẳng ấy. Vẽ về một phía của AB các tam giác đều AMC, BMD. Trung điểm I của CD chuyển động trên đường nào?
Giải bởi qa.haylamdo.com
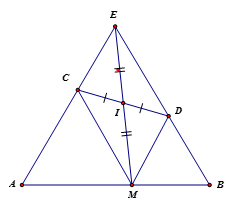
Gọi E là giao điểm của AC và BD ta có đều nên E là điểm cố định.
Lại có ECMD là hình bình hành nên trung điểm I của CD cũng là trung điểm của EM .
Theo bài 3, Mchuyển động trên đoạn thẳng AB thì I chuyển động trên đường trung bình của ( đoạn thẳng nối trung điểm của EA và EB )
Ghép mỗi ý (1), (2), (3), (4) với một trong các ý (a), (b), (c), (d) để được một khẳng định đúng:
|
(1) Tập hợp đỉnh A của tam giác cân ABC có đáy BC cố định … (2) Tập hợp các điểm cách đều hai đầu của một đoạn thẳng AB cố định... (3) Tập hợp đỉnh A của tam giác vuông ABC có cạnh huyền BC cố định ... (4) Tập hợp giao điểm của các đường chéo của các hình chữ nhật ABCD có cạnh CD cố định … |
|
(a) là đường trung trực của đoạn thẳng AB. (b) là đường trung trực của CD trừ trung điểm của CD (c) là đường trung trực của BC trừ trung điểm của BC (d) là đường tròn với O là trung điểm của BC. |
Cho tam giác ABC cân tại A. Các điểm D, E theo thứ tự chuyển động trên cạnh AB, AC sao cho AD = AE. Trung điểm I của đoạn thẳng DE di chuyển trên đường nào?
Cho vuông tại A có đường cao AH, M là một điểm di động trên cạnh BC. Gọi I là hình chiếu của M trên AB. Trên cạnh AC lấy điểm K sao cho IK = AM. Chứng minh tứ giác AIMK là hình chữ nhật.
Điền vào chỗ trống (…):
a) Tập hợp các điểm cách điểm A cố định một khoảng 5cm...
Cho tam giác ABC và một điểm M nằm trên cạnh BC. Khi điểm M di chuyển trên cạnh BC thì trung điểm I của đoạn thẳng AM di chuyển trên đường nào?
Cho điểm A nằm ngoài đường thẳng d. Điểm M di chuyển trên đường thẳng d. Gọi B là điểm đối xứng với A qua M. Điểm B di chuyển trên đường nào?
Cho đoạn thẳng AB, điểm M chuyển động trên đoạn thẳng ấy. Vẽ về một phía của AB các tam giác AMC vuông cân tại C, BMD vuông cân tại D. Trung điểm I của CD chuyển động trên đường nào?
