Giải bởi qa.haylamdo.com
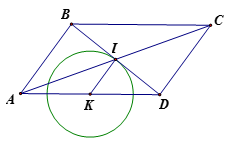
+ Gọi K là trung điểm AD. Ta có AD cố định nên K cố định
+ Trong ta có
IB = ID ( tính chất hình bình hành)
KA = KD ( theo cách vẽ)
Nên KI là đường trung bình của
Suy ra KI = AB : 2 = 2 : 2 = 1 (tính chất đường trung bình)
+ B , C thay đổi thì I thay đổi luôn cách K cố định một khoảng không đổi nên I chuyển động trên đường tròn (K,1cm)
Vậy B chuyển động trên đường thẳng xy song song với d cách d một khoảng bằng AKCho tam giác ABC cân tại A, các điểm M, N theo thứ tự di động trên các cạnh AB, AC sao cho AM = CN. Hãy tìm tập hợp trung điểm I của MN
Cho góc vuông xOy và điểm A thuộc tia Ox sao cho OA = 4cm. lấy điểm B tùy ý trên tia Oy và gọi M là trung điểm của AB . Khi B di chuyển trên tia Oy thì M di chuyển trên đường nào
Cho điểm A ở ngoài đường thẳng d và có khoảng cách đến d bằng 2cm. Trên d lấy một điểm B bất kì. Gọi C là điểm đối xứng với điểm A qua điểm B . Hỏi khi điểm B di chuyển trên đường thẳng d thì điểm C di chuyển trên đường nào?
Cho ABC có D là trung điểm của AB, kẻ DE // BC . Chứng minh rằng AE = EC.
Cho điểm A nằm ngoài đường thẳng d . Điểm M di chuyển trên đường thẳng d . Gọi B là điểm đối xứng với A qua M. Điểm B di chuyển trên đường nào?
