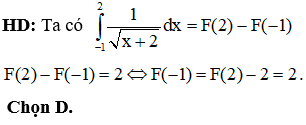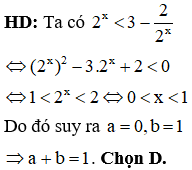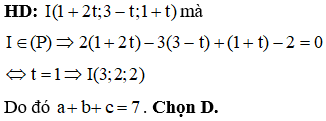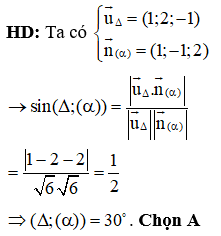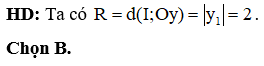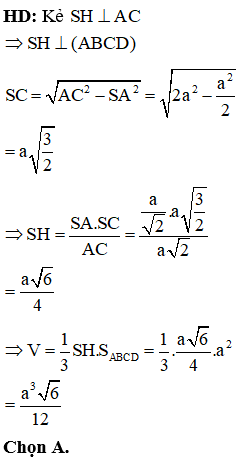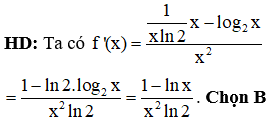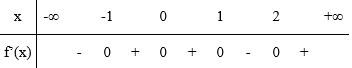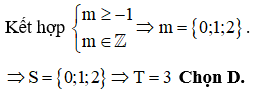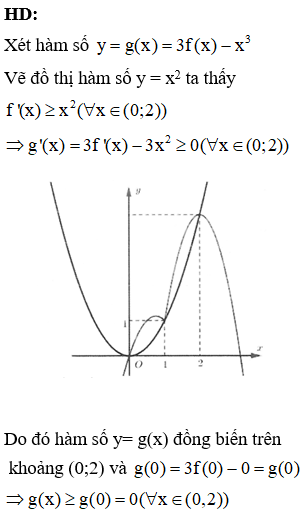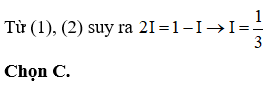30 đề thi thử thpt năm 2020 môn Toán cực hay có lời giải chi tiết
30 đề thi thử thpt năm 2020 môn Toán cực hay có lời giải chi tiết (đề số 27)
-
20012 lượt thi
-
50 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 3:
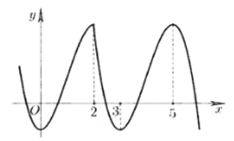
Cho hàm số y = f(x) có tập xác định và bảng biến thiên như hình vẽ
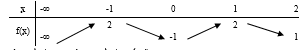
Mệnh đề nào sau đây sai về hàm số đã cho ?
HD: Đồ thị hàm số chỉ có 1 điểm cực tiểu là (0;-1) nên đáp án B sai. Chọn B.
Câu 8:
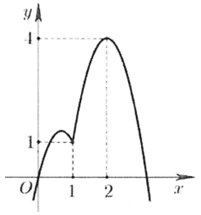
Cho hàm số y = f(x) có đồ thị như hình vẽ bên.
Hàm số đồng biến trên khoảng nào sau đây?

HD: Hàm số đã cho đồng biến trên (1;3) nên cũng đồng biến trên (2;3). Chọn C.
Câu 9:
Đường cong ở hình bên là đồ thị của hàm số nào dưới đây?
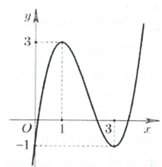
HD: Dựa vào hệ số α > 0 ta loại được đáp án C. Đồ thị cắt trục tung tại y = -1 nên loại B. Từ đồ thị ta thấy hàm số có hai điểm cực trị
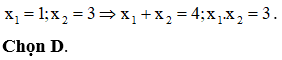
Câu 11:
Trong không gian Oxyz, mặt phẳng nào trong các mặt phẳng sau song song với trục Oz ?
HD: Mặt phẳng song song với trục Oz là (Q): x + 11y + 1 = 0. Đường thẳng Oz nằm trong mặt phẳng (P): x + y = 0 nên đáp án B không đúng. Chọn C.
Câu 13:
Mệnh đề nào sau đây sai?
HD: Số cách chọn và xếp thứ tự 4 học sinh từ nhóm 6 học sinh là nên đáp án C sai. Chọn C.
Câu 16:
Đồ thị hàm số có bao nhiêu đường tiệm cận?
HD: Đồ thị hàm số có 2 tiệm cận ngang là y = 2 và y = 0, không có TCĐ. Chọn C.
Câu 18:
Cho hàm số y = f(x) có đạo hàm với mọi . Giá trị nhỏ nhất của hàm số y = f(x) trên đoạn [-1 ;2] là
HD: Giá trị nhỏ nhất của hàm số là f (0). Chọn B.
Câu 23:
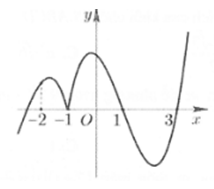
Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số và trục hoành như hình vẽ bên.
Mệnh đề nào sau đây sai ?
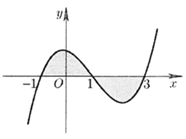
HD: Từ hình vẽ dễ thấy đáp án A, D đúng.
Đáp án B sai do kết quả của tích phân
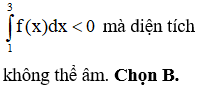
Câu 25:
Cho hình nón đỉnh S có đường sinh bằng 2, đường cao bằng 1. Tìm đường kính của mặt cầu chứa điểm S và chứa đường tròn đáy hình nón đã cho.

HD: Ta có tâm I của mặt cầu chính là tâm đường tròn ngoại tiếp tam giác SAB.
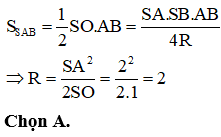
Câu 29:
Trong không gian Oxyz, cho đường thẳng ∆ đi qua điểm M(1;2;3) và có vec tơ chỉ phương là . Phương trình nào sau đây không phải là của đường thẳng ∆?
HD: Ta có
Cả 4 đáp án đều thỏa mãn về VTCP, ta xét điểm đi qua.
Thay tọa độ (-5;-10;-15),(2;4;6),(1;2;3),(3;6;12) vào phương trình
![]()
thì ta thấy (3;6;12) không thỏa mãn. Chọn D.
Câu 31:
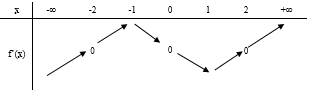
Cho hàm số y = f(x). Hàm số y’ = f’(x) có bảng biến thiên như hình vẽ bên. Hàm số g(x) = f(x) – x có bao nhiêu điểm cực trị ?
![]()

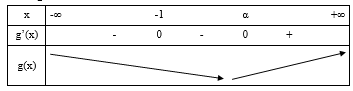
Hàm số đạt cực trị tại x = a. Chọn D.
Câu 34:
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B với . Tính theo a khoảng cách giữa hai đường thẳng AC, SD.

HD: Gọi I là trung điểm của AD → ABCI là hình vuông cạnh a → ∆ACI có đường trung tuyến
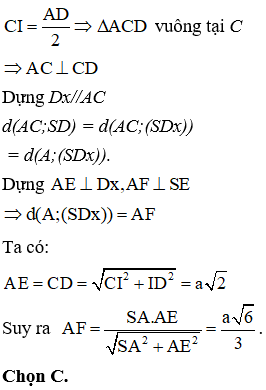
Câu 35:
Người ta sản xuất một vật lưu niệm (N) bằng thủy tinh trong suốt có dạng khối tròn xoay mà thiết kế qua trục của nó là một hình thang cân (xem hình vẽ). Bên trong (N) có hai khối cầu ngũ sắc với bán kính lần lượt là R= 3cm, r = 1cm tiếp xúc với nhau và cùng tiếp xúc với mặt xung quanh của (N), đồng thời hai khối cầu lần lượt tiếp xúc với hai mặt đáy của (N). Tính thể tích của vật lưu niệm đó
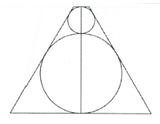

HD: Giả sử thiết diện là hình thang ABPQ
Gọi I, K lần lượt là tâm của đường tròn nhỏ và to.
Gọi M, N là hình chiếu của I, K lên một cạnh bên, điểm


Câu 39:
Trong Lễ tổng kết Tháng thanh niên, có 10 đoàn viên xuất sắc gồm 5 nam và 5 nữ được tuyên dương khen thưởng. Các đoàn viên này được sắp xếp ngẫu nhiên thành một hàng ngang trên sân khấu để nhận giấy khen. Tính xác suất để trong hàng ngang trên không có bất kì 2 bạn nữ nào đứng cạnh nhau
HD: Xếp 10 học sinh thành 1 hàng ngang có:
![]()
Gọi A là biến cố: “Hàng ngang không có 2 bạn nữ nào đứng cạnh nhau”
Sắp xếp 5 bạn nam thành 1 hàng có: 5! cách sắp xếp, khi đó có 6 vị trị để xếp 5 bạn nữ xen kẽ để không có hai bạn nữ đứng cạnh nhau (6 vị trí bao gồm 2 vị trí đầu và cuối và 4 vị trí giữa 2 bạn nam)
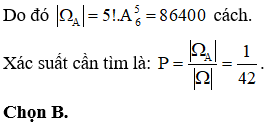
Câu 43:
Một biển quảng cáo có dạng hình Elip với bốn đỉnh , như hình vẽ bên. Người ta chia Elip bởi Parabol có đỉnh B1, trục đối xứng B1B2, và đi qua các điểm M ,N. Sau đó sơn phần tô đậm với giá 200.000 đồng/m2 và trang trí đèn Led phần còn lại với giá 500.000 đồng/m2. Hỏi kinh phí sử dụng gần nhất với giá trị nào dưới đây? Biết rằng A1A2 = 4m, B1B2 = 2m, MN = 2m

HD: Chọn hệ tọa độ Oxy, với O là trung điểm A1A2


Câu 44:
Sau khi tốt nghiệp, anh Nam thực hiện một dự án khởi nghiệp. Anh vay vốn từ ngân hàng 200 triệu đồng với lãi suất 0,6%/tháng. Phương án trả nợ của anh Nam là: sau đúng một tháng kể từ thời điểm vay anh bắt đầu trả nợ, hai lần trả nợ liên tiếp cách nhau đúng một tháng, số tiền trả của mỗi lần là như nhau và hoàn thành sau đúng 5 năm kể từ khi vay. Tuy nhiên, sau khi dự án có hiệu quả và đã trả nợ được 12 tháng theo phương án cũ anh Nam muốn rút ngắn thời gian trả nợ nên từ tháng tiếp theo, mỗi tháng anh trả nợ cho ngân hàng 9 triệu đồng. Biết rằng mỗi tháng ngân hàng chỉ tính lãi trên số dư nợ thực tế của tháng đó. Hỏi sau ít nhất bao nhiêu tháng từ thời điểm vay anh Nam trả hết nợ?

Sau khi gửi được 12 tháng theo kế hoạch cũ, số tiền anh Nam còn nợ là
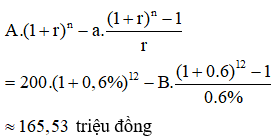
Theo kế hoạch mới thì tháng cuối anh Nam còn nợ 0 đồng và trả hàng tháng 9 triệu đồng

Câu 46:
Trong không gian Oxyz, cho tam giác ABC vuông tại A, , đường thẳng BC có phương trình , đường thẳng AB nằm trong mặt phẳng . Biết đỉnh C có cao độ âm. Tính hoành độ của đỉnh A.
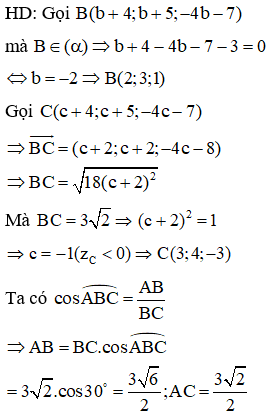
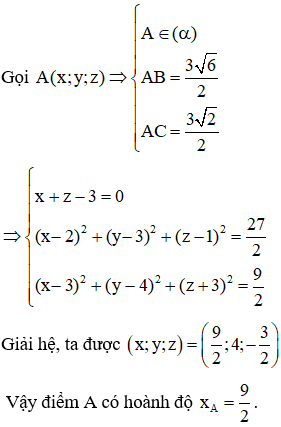
Chọn C.
Câu 47:
Trong không gian Oxyz, cho mặt cầu và điểm A(-2;0;-2). Từ A kẻ các tiếp tuyến đến (S) với các tiếp điểm thuộc đường tròn (ω). Từ điểm M di động nằm ngoài (S) và nằm trong mặt phẳng chứa (ω) kẻ các tiếp tuyến đến (S) với các tiếp điểm thuộc đường tròn (ω'). Biết rằng khi hai đường tròn (ω), (ω') có cùng bán kính thì M luôn thuộc một đường tròn cố định. Tìm bán kính r của đường tròn đó.
HD: Hình vẽ tham khảo
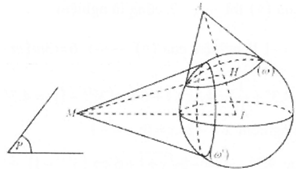

Câu 48:
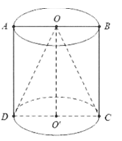
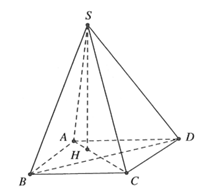
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh 2a, , SAB là tam giác đều, . Tính thể tích của khối chóp S.ABCD
HD: Gọi H là tâm đường tròn ngoại tiếp ∆SBD


Bán kính đường tròn ngoại tiếp ∆SBD là