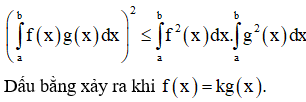50 câu hỏi trắc nghiệm thuộc 30 đề thi thử thpt năm 2020 môn Toán cực hay có lời giải chi tiết (đề số 19)

Câu 1:

Cho số phức $z = 3 - 4 i$ . Phần thực và phần ảo số phức z là

A. Phần thực bằng 3 và phần ảo bằng -4i

B. Phần thực bằng 3 và phần ảo bằng 4.

C. Phần thực bằng 3 và phần ảo bằng 4i

D. Phần thực bằng 3 và phần ảo bằng -4.

Chọn D.

Phương pháp: Đây là câu hỏi nhận biết về phần thực phần ảo của số phức ta dựa hoàn toàn vao định nghĩa phần thực và phần ảo số phức.

Cách giải: Dễ thấy phương án D là đáp án đúng.

Câu 2:

Tính giới hạn của dãy số $(u_{n})$ biết $u_{n} = \frac{n^{2} - 3 n^{3}}{2 n^{3} + 5 n - 2}$

A. $- \frac{3}{2}$

B. $\frac{3}{2}$

C. $\frac{1}{2}$

D. $\frac{1}{5}$

Xem đáp án

Chọn A.

Phương pháp: Giới hạn dạng vô cùng trên vô cùng ta chia cả tử và mẫu cho n với bậc cao nhất.

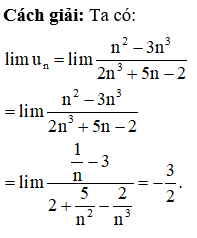
Câu 3:

Cho các số tự nhiên m, n thỏa mãn đồng thời các điều kiện $C_{m}^{2} = 153$ và $C_{m}^{n} = C_{m}^{n + 2}$ . Khi đó m+n bằng

A. 25

B. 27

C. 26

D. 23

Xem đáp án

Chọn C.

Phương pháp: Giải các phương trình đã cho.

Cách giải: Ta có:

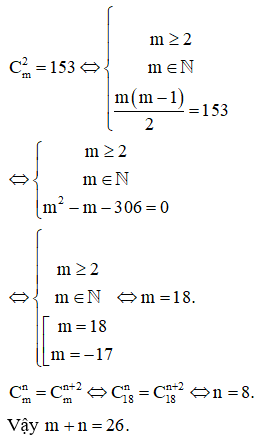
Câu 4:

Khối 8 mặt đều thuộc loại khối đa diện loại nào sau đây.

A. {3;3}

B. {4;3}

C. {5;3}

D. {3;4}

Xem đáp án

Chọn D.

Phương pháp: Đây là câu hỏi về lý thuyết đã có trong sách giáo khoa.

Cách giải: Chọn D.

Câu 5:

Cho hàm số $y = f (x)$ xác định, liên tục trên đoạn $[- 2; 2]$ và có đồ thị là đường cong ở hình vẽ bên.

Điểm cực đại của hàm số $y = f (x)$ là

A. -2

B. -1

C. 1

D. 2

Xem đáp án

Chọn B

Phương pháp: Dựa vào đồ thị hàm số.

Cách giải: Chọn B.

Câu 6:

Tìm nguyên hàm của hàm số $f (x) = \sin 3 x$

A. $\int_{}^{} f (x) d x = \frac{1}{3} \cos 3 x + C$

B. $\int_{}^{} f (x) d x = - \frac{1}{3} \cos 3 x + C$

C. $\int_{}^{} f (x) d x = 3 \cos 3 x + C$

D. $\int_{}^{} f (x) d x = - 3 \cos 3 x + C$

Xem đáp án

Chọn B.

Câu 7:

Tính tổng tung độ của các điểm cực tiểu của đồ thị hàm số $y = x^{4} - 2 x^{2} + 2$

A. 2

B. 2

C. 3

D. 4

Xem đáp án

Chọn B.

Phương pháp: Tìm tung độ các điểm cực tiểu.

Lưu ý: Tung độ điểm cực tiểu của hàm trùng phương (nếu có) bằng nhau.

Cách giải: Ta có:

Câu 8:

Cho hàm số $y = 2 \ln (\ln x) - \ln 2 x$ . Tính giá trị của y'(e)

A. $\frac{1}{e}$

B. $\frac{2}{e}$

C. $\frac{e}{2}$

D. $\frac{1}{2 e}$

Xem đáp án

Chọn A.

Phương pháp: Tính đạo hàm và thay x = e

Cách giải: Ta có:

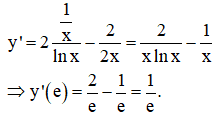
Câu 9:

Diện tích của hình phẳng giới hạn bởi parabol $y = 2 - x^{2}$ và đường thẳng $y = - x$ là

A. $S = \frac{9}{4}$

B. $S = \frac{9}{2}$

C. S = 9

D. S = 18

Xem đáp án

Chọn B.

Phương pháp: Tìm hoành độ giao điểm và lấy tích phân để tích diện tích.

Cách giải: Phương trình hoành độ giao điểm là:

Câu 10:

Trong không gian với hệ trục tọa độ Oxyz, cho điểm $M (8; - 2; 4)$ Viết phương trình mặt phẳng đi qua các điểm là hình chiếu vuông góc của điểm M lên các trục tọa độ.

A. $x + 4 y + 2 z - 8 = 0$

B. $x - 4 y + 2 z - 8 = 0$

C. $x - 4 y + 2 z = 0$

D. $8 x - 2 y + 4 z - 76 = 0$

Xem đáp án

Chọn B.

Phương pháp: Kinh nghiệm: Chiếu lên trục, mặt phẳng đặc biệt thì thiếu gì thì cho đấy bằng 0.

Sau đó dùng phương trình mặt phẳng theo đoạn chắn để viết.

Câu 11:

Cho hàm số $y = \frac{a x - 1}{b x + 2}$ . Xác định a và b để đồ thị hàm số nhận đường thẳng $x = 2$ là tiệm cận đứng và đường thẳng $y = - 1$ làm tiệm cận ngang.

A. $a = 2, b = - 3$

B. $a = 2, b = - 2$

C. $a - 1, b = 1$

D. $a = 1, b = - 1$

Xem đáp án

Chọn D.

Phương pháp: Sử dụng định nghĩa tiệm cận đứng.

Cách giải: Để đồ thị hàm số đã cho có tiệm cận đứng và tiệm cận ngang thì

Câu 12:

Trong không gian với hệ tọa độ Oxyz, cho hai điểm $A (1; 2; 2), B (3; - 2; 0)$ . Viết phương trình mặt phẳng trung trực của đoạn AB.

A. $x - 2 y - 2 z = 0$

B. $x - 2 y - z - 1 = 0$

C. $x - 2 y - z = 0$

D. $x - 2 y + z - 3 = 0$

Xem đáp án

Chọn B.

Phương pháp: Mặt phẳng trung trực đi qua trung điểm của đoạn thẳng và vuông góc với đoạn thẳng.

Câu 13:

Trong các hàm số được cho dưới đây, hàm số nào có tập xác định D = R.

A. $y = \ln (x^{2} - 1)$

B. $y = \ln (1 - x^{2})$

C. $y = \ln {(x + 1)}^{2}$

D. $y = \ln (x^{2} + 1)$

Xem đáp án

Chọn D.

Phương pháp: Tìm tập xác định.

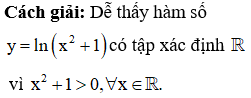
Câu 14:

Một hình trụ có chu vi của đường tròn đáy là c, chiều cao của hình trụ gấp 4 lần chu vi đáy. Thể tích của khối trụ này là

A. $\frac{2 c^{2}}{π^{2}}$

B. $\frac{2 c^{3}}{π}$

C. $4 π c^{3}$

D. $\frac{c^{3}}{π}$

Xem đáp án

Chọn D.

Phương pháp: Tìm bán kinh đáy từ đó tính thể tích khối trụ.

Cách giải: Gọi r là bán kính đáy.

Câu 15:

Trong không gian với hệ tọa độ Oxyz, cho $A (2; 0; 0), B (0; 4; 0), C (0; 0; 6)$ và $D (2; 4; 6)$ . Khoảng cách từ D đến mặt phẳng (ABC) là

A. $\frac{24}{7}$

B. $\frac{16}{7}$

C. $\frac{8}{7}$

D. $\frac{12}{7}$

Xem đáp án

Chọn A.

Phương pháp: Viết phương trình mặt phẳng (ABC) và tính khoảng cách.

Cách giải: Ta có:

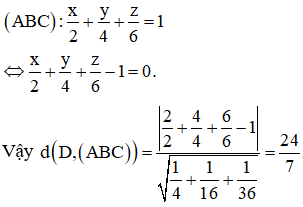
Câu 16:

Cho hàm số y = f(x) liên tục trên R và có bảng biến thiên như hình vẽ. Tìm tất cả các giá trị thực của m để phương trình $f (x) = 2 m$ có đúng hai nghiệm phân biệt.

A. m = 0 hoặc m < -3

B. m < -3

C. m = 0 hoặc $m < - \frac{3}{2}$

D. $m < - \frac{3}{2}$

Xem đáp án

Chọn C.

Phương pháp: Dựa vào bảng biến thiên để kết luận.

Cách giải: Dựa vào bảng biến thên suy ra để phương trình f(x) = 2m có đúng hai nghiệm phân biệt thì

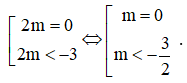
Câu 17:

Tiếp tuyến của đồ thị hàm số $y = f (x) = x^{3} - 3 x^{2} + 2$ tại điểm có hoành độ bằng -1 có phương trình là

A. y = 9x + 7

B. y = 9x - 11

C. y = -3x - 5

D. y = -9x +

Xem đáp án

Chọn A.

Phương pháp: Viết phương trình tiếp tuyến theo công thức

Câu 18:

Đường cong trong hình bên là đồ thị của một trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào

A. $y = - x^{4} + 8 x^{2} + 1$

B. $y = x^{4} - 8 x^{2} + 1$

C. $y = - x^{3} + 3 x^{2} + 1$

D. $y = - x^{3} + 3 x^{2} + 1$

Xem đáp án

Chọn D.

Phương pháp: Sử dụng hình dáng đồ thị và các điểm đặc biệt có trên đồ thị.

Cách giải: Dựa vào hình dáng đồ thị ta loại các phướng án A, C.

Thay tọa độ điểm (2;-3) ta loại được B.

Vậy D. là đáp án.

Câu 19:

Cho hàm số y = f(x) liên tục trên R thỏa mãn $\int_{0}^{4} f (x) d x = 8$ . Tính $I = \int_{0}^{2} f (2 x) d x$

A. 9

B. 8

C. 4

D. 1

Xem đáp án

Chọn C.

Phương pháp: Sử dụng phương pháp đổi biến.

Cách giải: Ta có:

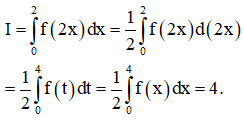
Câu 20:

Tập hợp tất cả các điểm biểu diễn số phức z thỏa mãn điều kiện $|z - i| = |2 - 3 i - z|$ là

A. Một đường tròn

B. Một đường Elip.

C. Một đường thẳng.

D. Một đoạn thẳng.

Xem đáp án

Chọn C.

Phương pháp: Biến đổi đẳng thức đã cho.

Cách giải: Giả sử

Vậy tập hợp tất cả các điểm biểu diễn số phức z thỏa mãn điều kiện $|z - i| = |2 - 3 i - z|$ là một đường thẳng.

Câu 21:

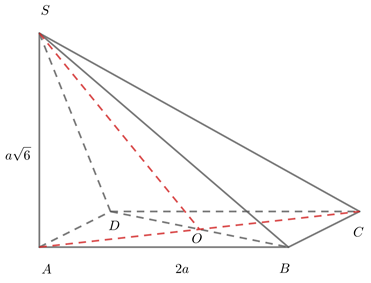
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, SA vuông góc với đáy, $S A = a \sqrt{6}$ . Góc giữa hai mặt phẳng (SBD) và mặt phẳng (ABCD) là

A. $45 °$

B. $90 °$

C. $60 °$

D. $30 °$

Xem đáp án

Chọn C.

Phương pháp: Muốn xác định góc giữa hai mặt phẳng ta thực hiện các bước sau:

Xác định giao tuyến của hai mặt phẳng đó.

Lấy 1 điểm nằm trên giao tuyến.

Dựng 2 đường thẳng lần lượt nằm trong hai mặt phẳng đi qua điểm và vuông góc với giao tuyến.

Góc giữa hai đường thẳng chính là góc giữa hai mặt phẳng.

Cách giải: Gọi O là giao điểm của AC và BD.

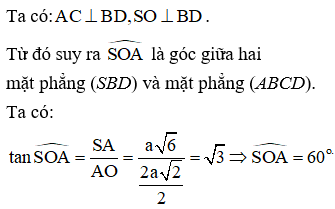
Câu 22:

Tích tất cả các nghiệm của phương trình $\log_{2}^{2} x + \sqrt{\log_{2} x + 1} = 1$

A. $2^{\frac{- 1 - \sqrt{5}}{2}}$

B. 1

C. $2^{\frac{1 - \sqrt{5}}{2}}$

D. $\frac{1}{2}$

Xem đáp án

Chọn A.

Phương pháp: Viết điều kiện và giải phương trình đã cho.

Cách giải: Điều kiện xác định của phương trình là:

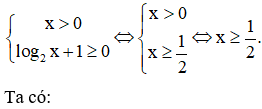
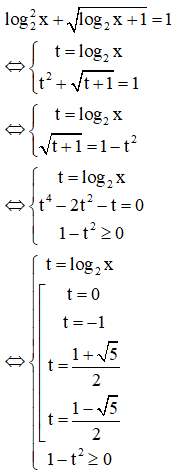
Câu 23:

Một hội đồng quản trị của một công ty gồm 12 người, trong đó có 5 nữ. Từ hội đồng quản trị đó người ta bầu ra 1 chủ tịch, 1 phó chủ tịch và 2 ủy viên. Hỏi có bao nhiêu cách bầu sao cho trong 4 người được bầu phải có nữ.

A. 410.

B. 1188.

C. 5940.

D. 5520.

Xem đáp án

Chọn D.

Phương pháp: Đếm bằng tổ hợp.

Cách giải:

Lần lượt chọn ra 1 người làm chủ tịch, một người làm phó chủ tịch và 2 ủy viên.

Gọi A là biến cố:” Trong 4 người được bầu phải có nữ”.

$\bar{A}$ là biến cố:” Trong 4 người được bầu không có nữ”.

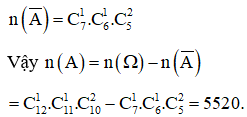
Câu 24:

Trong không gian với hệ trục tọa độ Oxyz, cho bốn điểm $A (1; 1; 1), B (3; 2; 1), C (7; 3; 5), D (4; 6; 2)$ . Viết phương trình mặt phẳng chứa AB và song song với CD

A. $x + y + 2 z + 4 = 0$

B. $x - 2 y - 3 z + 4 = 0$

C. $x - 2 y - 3 z - 4 = 0$

D. $x + y + z + 4 = 0$

Xem đáp án

Chọn B.

Phương pháp: Một véc tơ pháp tuyến của mặt phẳng cần viết phương trình là tích có hướng của $\vec{A B} v à \vec{C D}$

là một véc tơ pháp tuyến của mặt phẳng

chứa AB và song song với CD.

Vậy phương trình mặt phẳng cần tìm là:

Câu 25:

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, P theo thứ tự là trung điểm của SA, SD và AB. Khẳng định nào sau đây đúng?

A. MON cắt (OPM).

B. (MON)//(SBC)

C. $(P O N) \cap (M N P) = N P$

D. (NMP)//(SBD)

Xem đáp án

Chọn B.

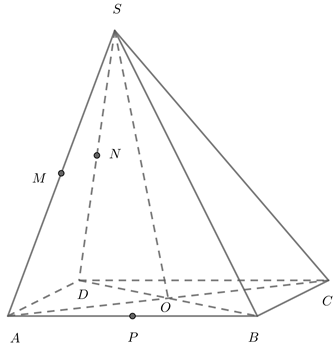
Phương pháp: Xét tính đúng sai của từng mệnh đề.

Cách giải: Ta có 4 điểm M, N, O, P đồng phẳng.

Câu 26:

Tìm hệ số của $x^{5}$ trong khai triển $P (x) = (1 + x) + 2 {(1 + x)}^{2} + . . . + 8 {(1 + x)}^{8}$

A. 638

B. 663

C. 636

D. 634

Xem đáp án

Chọn C.

Câu 27:

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, $S A ⊥ (A B C D), S A = a \sqrt{6}$ . Khoảng cách từ A đến mặt phẳng (SDB) là

A. $\frac{a \sqrt{13}}{3}$

B. $\frac{a \sqrt{6}}{\sqrt{13}}$

C. $\frac{a \sqrt{13}}{6}$

D. $\frac{a \sqrt{6}}{\sqrt{7}}$

Xem đáp án

Chọn B.

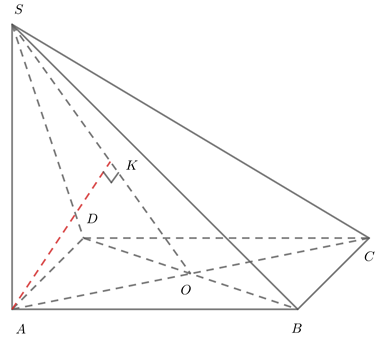
Phương pháp: Xác định hình chiếu của A lên (SBD)

Cách giải: Gọi O là giao điểm của AC và BD.

K là hình chiếu của A lên SO.

Câu 28:

Trong không gian với hệ tọa độ Oxyz, cho các điểm $A (- 1; 0; 1), B (1; 1; - 1), C (5; 0; - 2)$ . Tìm tọa độ điểm H sao cho tứ giác ABCH là thành hình thang cân với hai đáy AB, CH.

A. H(3;-1;0)

B. H(7;1;-4)

C. H(-1;-3;4)

D. H(1;-2;2)

Xem đáp án

Chọn C.

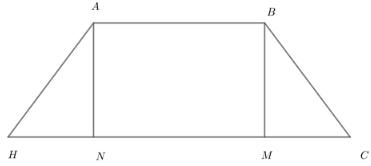
Phương pháp: Sử dụng các véc tơ bằng nhau.

Giả sử M,N lần lượt là hình chiếu của A, B lên CH.

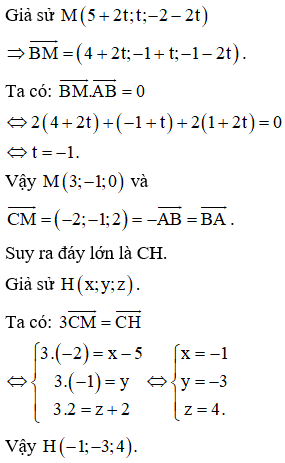
Câu 29:

Tìm tất cả các giá trị thực của tham số m để hàm số $y = x e^{x^{2} + m x - 2}$ có cực trị

A. $m \in ℝ$

B. $m > 2 \sqrt{2}$

C. $m \neq 0$

D. $|m| > 2 \sqrt{2}$

Xem đáp án

Chọn D.

Phương pháp: Tính đạo hàm và tìm điều kiện để hàm số có cực trị.

Cách giải: Ta có:

Câu 30:

Cho hàm số $y = x^{4} - m x^{2} + m$ (với m là tham số) có đồ thị là (C). Biết rằng khi $m = m_{0}$ đồ thị (C) cắt trục hoành tại 4 điểm phân biệt có hoành độ $x_{1}, x_{2}, x_{3}, x_{4}$ thỏa mãn ${x_{1}}^{4} + {x_{2}}^{4} + {x_{3}}^{4} + {x_{4}}^{4}$ . Hỏi mệnh đề nào sau đây là đúng?

A. $4 \leq m_{0} \leq 7$

B. $- 2 < m_{0} < 4$

C. $m_{0} > 7$

D. $m_{0} \leq - 2$

Xem đáp án

Chọn A.

Phương pháp: Tìm m.

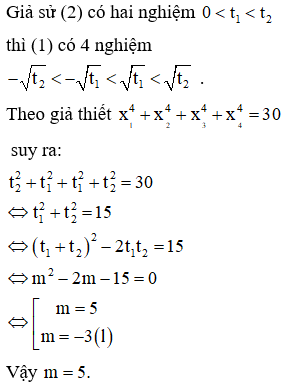
Câu 31:

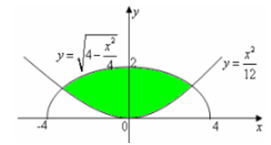
Cho hình phẳng (H) giới hạn bởi Parabol $y = \frac{x^{2}}{12}$ và đường cong có phương trình $y = \sqrt{4 - \frac{x^{2}}{4}}$ (như hình vẽ). Diện tích của hình phẳng (H) bằng

A. $\frac{4 π + \sqrt{3}}{3}$

B. $\frac{4 \sqrt{3} + π}{6}$

C. $\frac{4 π + \sqrt{3}}{6}$

D. $\frac{2 (4 π + \sqrt{3})}{3}$

Xem đáp án

Chọn D.

Phương pháp: Tìm cận và dùng tích phân để tính diện tích.

Cách giải: Ta có phương trình hoành độ giao điểm là

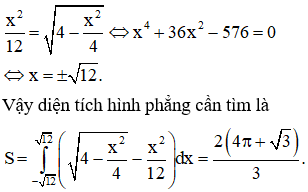
Câu 32:

Giả sử $\int_{1}^{2} \frac{\sqrt{1 + x^{2}}}{x^{4}} d x = \frac{1}{c} (a \sqrt{a} - \frac{b}{b + c} \sqrt{b}) (a; b; c \in ℕ; 1 \leq a, b, c \leq 9)$ . Tính giá trị biểu thức $S = C_{2 a + c}^{b - a}$ .

A. 165

B. 715

C. 5456

D. 35

Xem đáp án

Chọn D.

Phương pháp: Tính tích phân để suy ra a, b, c.

Cách giải: Ta có:

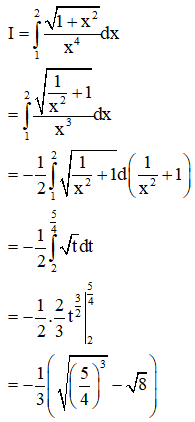
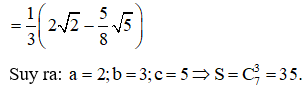
Câu 33:

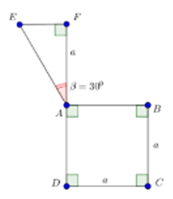
Tính thể tích của vật thể tròn xoay khi quay mô hình (như hình vẽ) quanh trục DF.

A. $\frac{10 {πa}^{3}}{9}$

B. $\frac{10 {πa}^{3}}{7}$

C. $\frac{5 {πa}^{3}}{2}$

D. $\frac{{πa}^{3}}{3}$

Xem đáp án

Chọn A.

Phương pháp: Ta thấy vật thể tròn xoay gồm 2 phần nón và trụ.

Cách giải:

Câu 34:

Trong tất cả các cặp (x;y) thỏa mãn $\log_{x^{2} + y^{2} + 2} (4 x + 4 y - 4) \geq 1$ . Tìm m để tồn tại duy nhất cặp (x;y) sao cho $x^{2} + y^{2} + 2 x - 2 y + 2 - m = 0$ .

A. ${(\sqrt{10} - \sqrt{2})}^{2}$

B. $\sqrt{10} - \sqrt{2} h o ặ c \sqrt{10} + \sqrt{2}$

C. ${(\sqrt{10} - \sqrt{2})}^{2} h o ặ c {(\sqrt{10} + \sqrt{2})}^{2}$

D. $\sqrt{10} - \sqrt{2}$

Xem đáp án

Chọn C.

Phương pháp: Đưa bài toán về tìm m để hệ có nghiệm duy nhất.

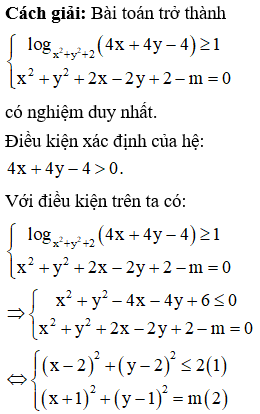
Câu 35:

Có bao nhiêu giá trị nguyên của tham số m để phương trình $\cos 3 x - \cos 2 x + m \cos x = 1$ có đúng 7 nghiệm khác nhau thuộc khoảng $(- \frac{π}{2}; 2 π)$

A. 2

B. 4

C. Không tồn tại

D. 1

Xem đáp án

Chọn D.

Phương pháp: Biện luận nghiệm của phương trình theo m.

Cách giải: Ta có:

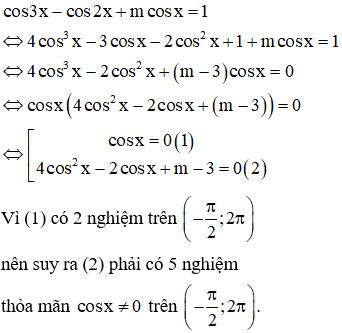
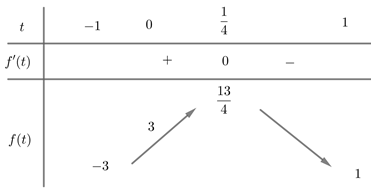
Câu 36:

Có tất cả bao nhiêu giá trị thực của tham số m để giá trị lớn nhất của hàm số $y = |x^{2} - 2 x + m|$ trên đoạn $[- 1; 2]$ bằng 5.

A. 3

B. 1

C. 2

D. 4

Xem đáp án

Chọn C.

Phương pháp: Biện luận theo m.

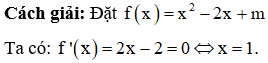
Câu 37:

Cho hàm số $y = f (x) = a x^{3} + b x^{2} + c x + d (a, b, c, d \in ℝ, a \neq 0)$ có đồ thị (C). Biết đồ thị (C) đi qua A(1;4) và đồ thị hàm số $y = f' (x)$ cho bởi hình vẽ

Giá trị $f (3) - 2 f (1)$ là

A. 6

B. 5

C. 28

D. 26

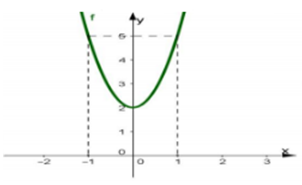
Xem đáp án

Chọn D.

Phương pháp: Tìm hàm số $y = f (x) = a x^{3} + b x^{2} + c x + d (a, b, c, d \in ℝ, a \neq 0)$

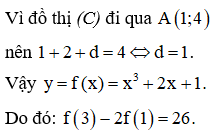
Câu 38:

Cho các số phức z, w thỏa mãn $|z + 2 - 2 i| = |z - 4 i|; w = i z + 1$ . Giá trị nhỏ nhất của $|w|$ là

A. $\frac{\sqrt{2}}{2}$

B. $2 \sqrt{2}$

C. $3 \sqrt{2}$

D. $\frac{5}{\sqrt{2}}$

Xem đáp án

Chọn A.

Phương pháp: Biến đổi đẳng thức

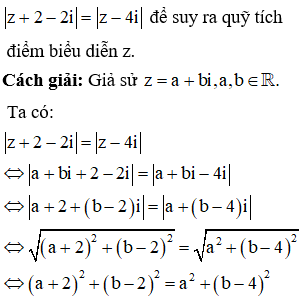
Câu 39:

Cho hàm số $y = f (x)$ có đạo hàm $f' (x) = {(x + 1)}^{4} {(x - 2)}^{5} {(x + 3)}^{3}$ . Số điểm cực trị của hàm số $y = f (|x|)$ là

A.5

B. 3

C. 2

D. 1

Xem đáp án

Chọn B.

Phương pháp: Biện luận theo số cực trị của f(x) và sử dụng phép suy đồ thị.

Cách giải: Ta có: f(x) đạt cực trị tại x = -3; x = -2

Vậy f(x) đạt cực trị tại một điểm bên phải trục Oy.

Câu 40:

Cho hàm số $y = f (x)$ liên tục trên đoạn $[- 2; 2]$ và có đồ thị là đường cong như trong hình vẽ bên

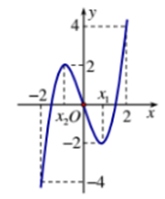
Hỏi phương trình $|f (x) - 1| = 2$ có bao nhiêu nghiệm phân biệt trên đoạn $[- 2; 2]$

A. 1

B. 3

C. 4

D. 2

Xem đáp án

Chọn C.

Phương pháp: Sử dụng phép suy đồ thị.

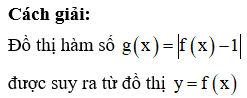
bằng cách tịnh tiến xuống 1 đơn vị, sau đó lấy đối xứng qua Ox và bỏ phần bên dưới Ox.

Câu 41:

Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng $(P) : a x + b y + c z - 9 = 0$ đi qua hai điểm $A (3; 2; 1), B (- 3; 5; 2)$ và vuông góc với mặt phẳng $(Q) : 3 x + y + z + 4 = 0$ . Tính tổng $S = a + b + c$

A. S = -12

B. S = 21

C. S = -4

D. S = 7

Xem đáp án

Chọn C.

Phương pháp: Lập hệ phương trình tìm a,b,c.

Cách giải: Từ giả thiết ta có hệ:

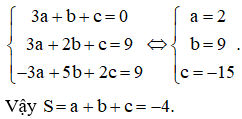
Câu 42:

Cho dãy số $(u_{n})$ được xác định như sau $\{\begin{cases} u_{1} = 2 \\ u_{n + 1} + 4 u_{n} = 4 - 5 n \end{cases} (n \geq 1)$ . Tính tổng $S = u_{2018} - 2 u_{2017}$

A. $S = 2015 - 3 . 4^{2017}$

B. $S = 2016 - 3 . 4^{2017}$

C. $S = 2017 + 3 . 4^{2017}$

D. $S = 2018 + 3 . 4^{2017}$

Xem đáp án

Chọn A.

Phương pháp:

Cách giải: Ta có:

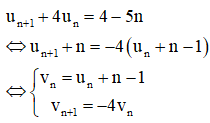
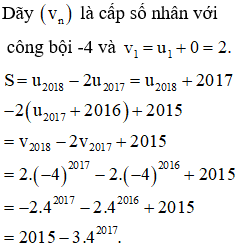
Câu 43:

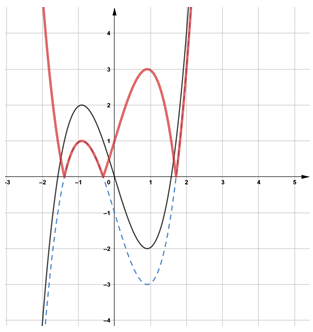
Biết rằng hàm số $y = f (x)$ có đồ thị được cho như hình vẽ bên.

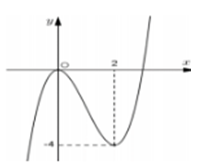
Tìm số điểm cực trị của hàm số $y = f [f (x)]$

A. 2

B. 3

C. 4

D. 0

Xem đáp án

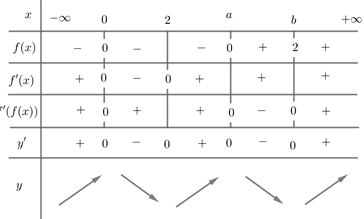
Chọn C.

Phương pháp: Sử dụng đạo hàm của hàm hợp.

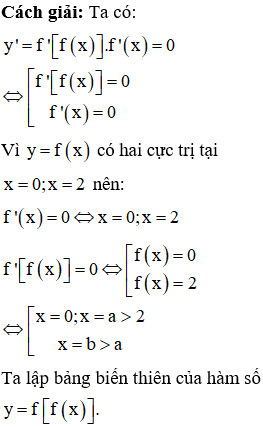
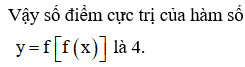
Câu 44:

Trong không gian với hệ tọa độ Oxyz, cho hai điểm $M (- 2; - 2; 1), A (1; 2; - 3)$ và đường thẳng $d : \frac{x + 1}{2} = \frac{y - 5}{2} = \frac{z}{- 1}$ . Tìm vectơ chỉ phương $\vec{u}$ của đường thẳng $∆$ đi qua M, vuông góc với đường thẳng d đồng thời cách điểm A một khoảng bé nhất

A. $\vec{u} = (- 2; 1; 0)$

B. $\vec{u} = (1; 0; 2)$

C. $\vec{u} = (0; 4; 1)$

D. $\vec{u} = (- 1; 1; 3)$

Xem đáp án

Chọn B.

Phương pháp: Gọi (P) là mặt phẳng đi qua M vuông góc với d.

Câu 45:

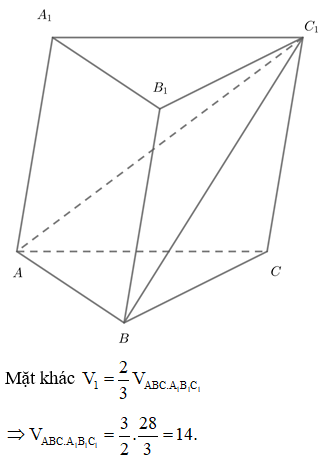
Cho hình lăng trụ $A B C A_{1} B_{1} C_{1}$ có diện tích mặt bên $A B B_{1} A_{1}$ bằng 4. Khoảng cách giữa cạnh $C C_{1}$ và mặt phẳng $(A B B_{1} A_{1})$ bằng 7. Tính thể tích khối lăng trụ $A B C A_{1} B_{1} C_{1}$ .

A. 14

B. 18

C. 9

D. 25

Xem đáp án

Chọn A.

Phương pháp: Chú ý

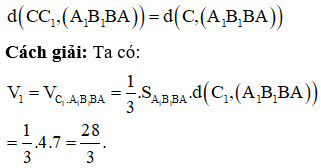
Câu 46:

Cho số phức z thỏa mãn $|z - 3 - 4 i| = \sqrt{5}$ . Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức $P = {|z + 2|}^{2} - {|z - i|}^{2}$ . Tính modum của số phức w = M + mi.

A. $|w| = \sqrt{2360}$

B. $|w| = \sqrt{1259}$

C. $|w| = \sqrt{1258}$

D. $|w| = 3 \sqrt{139}$

Xem đáp án

Chọn C.

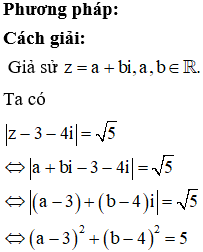
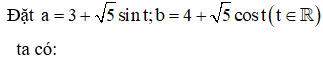
Câu 47:

Cho hình lập phương $A B C D . A' B' C' D'$ có cạnh bằng a. Gọi K là trung điểm của DD'. Khoảng cách giữa hai đường thẳng CK và A'D bằng

A. $\frac{a}{\sqrt{3}}$

B. $\frac{a}{2}$

C. $\frac{a}{6}$

D. $\frac{a}{3}$

Xem đáp án

Chọn D.

Phương pháp: Phương pháp tọa độ.

Cách giải: Chọn hệ trục tọa độ như hình vẽ, chọn a = 1

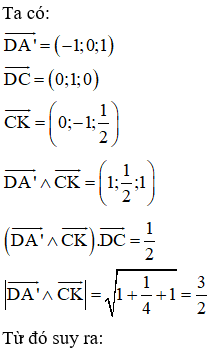
Câu 48:

Trong không gian với hệ tọa độ Oxyz, xét tứ diện ABCD có các cặp cạnh đối diện bằng nhau và điểm D khác phía với O so với mặt phẳng (ABC); đồng thời A, B, C lần lượt là giao điểm của các trục Ox, Oy, Oz và mặt phẳng $(α) : \frac{x}{m} + \frac{y}{m + 2} + \frac{z}{m - 5} = 1$ (với $m \neq - 2, m \neq 0, m \neq 5$ ). Tìm khoảng cách ngắn nhất từ tâm mặt cầu ngoại tiếp I của tứ diện ABCD đến O.

A. $\sqrt{20}$

B. $\frac{1}{4}$

C. $\sqrt{36}$

D. $\frac{\sqrt{26}}{2}$

Xem đáp án

Chọn D.

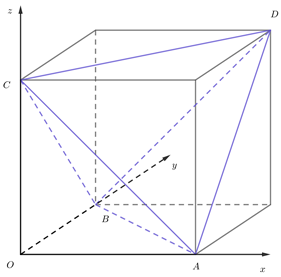
Phương pháp: Tứ diện ABCD có các cặp cạnh đối diện bằng nhau là tứ diện gần đều.

Cách giải: Theo giả thiết suy ra:

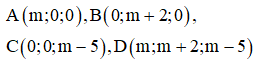
Theo tính chất của tứ diện gần đều tâm mặt cầu ngoại tiếp I của tứ diện ABCD là trung điểm OD

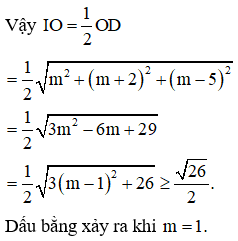
Câu 49:

Hai người ngang tài ngang sức tranh chức vô địch của một cuộc thi đá cầu. Người giành chiến thắng là người đầu tiên thắng được 5 trận cầu. Tại thời điểm người chơi thứ nhất đã thắng 4 trận cầu thì người chơi thứ hai mới thắng 2 trận cầu, tính xác suất để người chơi thứ nhất giành chiến thắng

A. $\frac{3}{5}$

B. $\frac{4}{7}$

C. $\frac{7}{8}$

D. $\frac{1}{3}$

Xem đáp án

Chọn C.

Phương pháp:

Cách giải: Để người thứ nhất thắng thì hoặc người thứ nhất thắng 1 ván hoặc người thứ 2 thắng ít hơn 3 ván.

Vậy xác suất để người chơi thứ nhất giành chiến thắng là

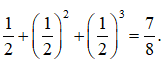
Câu 50:

Cho hàm số f(x) có đạo hàm dương, liên tục trên đoạn $[0; 1]$ thỏa mãn $f (0) = 1$ và $5 \int_{0}^{1} f' (x) {[f (x)]}^{2} d x + \frac{1}{5} \leq 2 \int_{0}^{1} \sqrt{f' (x)} f (x) d x$ . Tích phân $\int_{0}^{1} {[f (x)]}^{3} d x$

A. $\frac{1}{14}$

B. $\frac{2}{7}$

C. $\frac{54}{11}$

D. $\frac{53}{50}$

Xem đáp án

Chọn D.

Phương pháp: Áp dụng bất đẳng thức tích phân

CHỌN BỘ SÁCH BẠN MUỐN XEM

30 đề thi thử thpt năm 2020 môn Toán cực hay có lời giải chi tiết

30 đề thi thử thpt năm 2020 môn Toán cực hay có lời giải chi tiết (đề số 19)

Danh sách câu hỏi

Bài thi liên quan