Cho tam giác ABC cân tại A. Trên các cạnh bên AB, AC lấy các điểm M, N sao cho BM = CN. Tứ giác BMNC là hình gì? Chọn đáp án đúng nhất.
A. Hình thang.
B. Hình thang cân.
C. Hình thang vuông.
D. Cả A, B, C đều sai.
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Đáp án cần chọn là: B
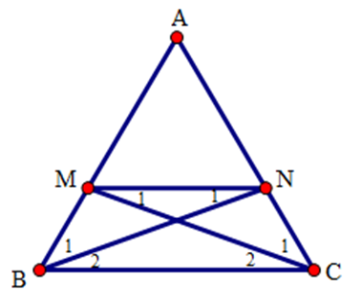
Ta có AB = AM + MB và AC = AN + NC
Mà AB = AC (do tam giác ABC cân tại A) và BM = NC (gt)
Suy ra AN = AM
Xét tam giác AMN cân tại A.
Suy ra .
Xét tam giác ANM có: (tổng ba góc trong một tam giác)
= (vì ) (1)
Xét tam giác ABC cân tại A ta có:
= (tổng ba góc trong một tam giác) nên = (vì ) (2)
Từ (1) và (2)
Mà , là hai góc đồng vị nên MN // BC
Xét tứ giác MNCB có MN // BC nên MNCB là hình thang.
Lại có (do ΔABC cân tại A) nên MNCB là hình thang cân.
Cho tam giác ABC cân tại A. Gọi D, E theo thứ tự thuộc các cạnh bên AB, AC sao cho AD = AE. Tứ giác BDEC là hình gì?
Chọn đáp án đúng nhất.
Cho hình thang cân MNPQ (MN // PQ) có góc và hai đáy có độ dài 8cm, 30cm. Diện tích của hình thang cân là:
Góc kề cạnh bên của hình thang có số đo là . Góc kề còn lại của cạnh bên đó là:
Cho tam giác ABC vuông tại A, đường cao AH. Trên BC lấy điểm M sao cho CM = CA. Đường thẳng đi qua M và song song với CA cắt AB tại I.
Chọn câu đúng nhất. Tứ giác ACMI là hình gì?
Cho hình thang vuông ABCD có , AB = AD = 2cm, DC = 4cm. Tính góc ABC của hình thang.
Cho hình thang cân MNPQ (MN // PQ) có góc và hai đáy có độ dài 12cm, 40cm. Diện tích của hình thang cân là:
Cho hình thang cân ABCD đáy nhỏ AB = 4cm, đáy lớn CD = 10cm, cạnh bên BC = 5cm thì đường cao AH bằng:
Cho hình thang cân ABCD (AB // CD) có hai đường chéo cắt nhau tại I, hai đường thẳng AD và BC cắt nhau ở K. Chọn khẳng định đúng:
Cho hình thang cân ABCD có đáy nhỏ AB = 4cm, đường AH = 6cm, và . Độ dài đáy lớn CD bằng
Cho hình thang ABCD có , DC = BC = 2.AB, DC = 4cm. Tính góc ABC của hình thang.
Cho hình thang cân ABCD có đáy nhỏ AB = 3cm, đường AH = 5cm, và . Độ dài đáy lớn CD bằng