Tìm giá trị nhỏ nhất của biểu thức \[P = 3\left( {\frac{{{a^2}}}{{{b^2}}} + \frac{{{b^2}}}{{{a^2}}}} \right) - 8\left( {\frac{a}{b} + \frac{b}{a}} \right)\].
A.\[ - \frac{{34}}{3}\]
B.4
C.22
D.−10
Giải bởi qa.haylamdo.com
Ta có :
\[{\left( {\frac{a}{b} + \frac{b}{a}} \right)^2} = \frac{{{a^2}}}{{{b^2}}} + 2\frac{a}{b}.\frac{b}{a} + \frac{{{b^2}}}{{{a^2}}} = \frac{{{a^2}}}{{{b^2}}} + \frac{{{b^2}}}{{{a^2}}} + 2 \Rightarrow \frac{{{a^2}}}{{{b^2}}} + \frac{{{b^2}}}{{{a^2}}} = {\left( {\frac{a}{b} + \frac{b}{a}} \right)^2} - 2\]
Biến đổi biểu thức P về dạng
\[P = 3{\left( {\frac{a}{b} + \frac{b}{a}} \right)^2} - 6 - 8\left( {\frac{a}{b} + \frac{b}{a}} \right) = 3{\left( {\frac{a}{b} + \frac{b}{a}} \right)^2} - 8\left( {\frac{a}{b} + \frac{b}{a}} \right) - 6\]
Đặt \[t = \frac{a}{b} + \frac{b}{a} \Rightarrow {t^2} = {\left( {\frac{a}{b} + \frac{b}{a}} \right)^2}\]
Áp dụng bất đẳng thức \[{\left( {x + y} \right)^2} \ge 4xy\,\,\forall x,y\] với hai số \[\frac{a}{b}\] và \[\frac{b}{a}\] ta có :
\[{t^2} = {(\frac{a}{b} + \frac{b}{a})^2} \ge 4\frac{a}{b}.\frac{b}{a} = 4 \Leftrightarrow |t| \ge 2 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{t \ge 2}\\{t \le - 2}\end{array}} \right.\]
Biểu thức P trở thành \[P = 3{t^2} - 8t - 6\]Trục đối xứng \[x = - \frac{b}{{2a}} = \frac{4}{3}\] và hệ số \[a = 3 >0.\]
Suy ra hàm số \[f\left( t \right) = 3{t^2} - 8t - 6\] nghịch biến trên khoảng \[\left( { - \infty ;\frac{4}{3}} \right)\] và đồng biến trên khoảng \[\left( {\frac{4}{3}; + \infty } \right)\]BBT :
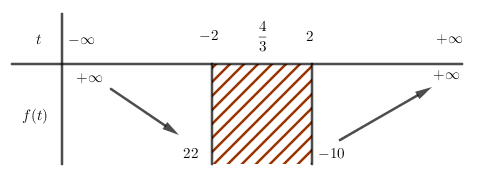
Từ đây suy ra hàm số f(t) đạt giá trị nhỏ nhất tại t = 2
Ta có f(2 )= −10.
Vậy minP = minf(t) = −10.
Đáp án cần chọn là: D
Tìm các giá trị thực của tham số m để phương trình \[\left| {{x^2} - 3x + 2} \right| = m\;\] có bốn nghiệm thực phân biệt.
Tìm các giá trị của tham số mm để phương trình \[{x^2} - 2(m + 1)x + 1 = 0\;\] có hai nghiệm phân biệt trong đó có đúng một nghiệm thuộc khoảng (0;1).
Tìm các giá trị của tham số m để phương trình \[\frac{1}{2}{x^2} - 4\left| x \right| + 3 = {m^2}\] có 3 nghiệm thực phân biệt.
Tìm các giá trị của m để hàm số \[y = {x^2} + mx + 5\;\] luôn đồng biến trên \[\left( {1; + \infty } \right)\]
Tìm giá trị của m để hàm số \[y = - {x^2} + 2x + m - 5\] đạt giá trị lớn nhất bằng 6
Cho đồ thị hàm số \[y = a{x^2} + bx + c\] như hình vẽ.
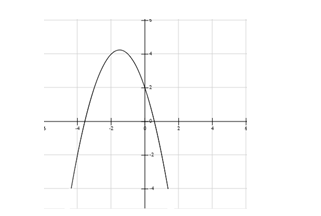
Khẳng định nào sau đây là đúng:
Xác định Parabol (P):\[y = a{x^2} + bx - 5\] biết rằng Parabol đi qua điểm A(3;−4) và có trục đối xứng x = −\(\frac{3}{2}\).
Xác định Parabol (P):\[y = a{x^2} + bx + 2\;\] biết rằng Parabol đi qua hai điểm M(1;5) và N(2;−2).
Xác định Parabol (P):\[y = a{x^2} + bx + 3\;\] biết rằng Parabol có đỉnh I(3;−2).
Tìm các giá trị của tham số m để phương trình \[2{x^2} - 2x + 1 - m = 0\;\]có hai nghiệm phân biệt
Tìm các giá trị của tham số m để \[2{x^2} - 2(m + 1)x + {m^2} - 2m + 4 \ge 0(\forall x)\]
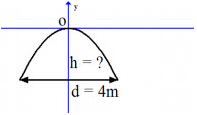
Một cái cổng hình parabol có dạng \[y = - \frac{1}{2}{x^2}\;\] có chiều rộng d = 4m.
Tính chiều cao h của cổng (xem hình minh họa)
Viết phương trình của Parabol (P) biết rằng (P) đi qua các điểm A(0;2),B(−2;5),C(3;8)
Tìm các giá trị của m để phương trình \[{x^2} - 2x + \sqrt {4{x^2} - 12x + 9} = m\] có nghiệm duy nhất.
Tìm giá trị của m để đồ thị hàm số \[y = {x^2} - 2x + m - 1\] cắt trục hoành tại hai điểm phân biệt có hoành độ dương.
