ĐGNL ĐHQG Hà Nội - Tư duy định lượng - Bài toán về đồ thị hàm số bậc hai
-
1227 lượt thi
-
22 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Cho đồ thị hàm số \[y = a{x^2} + bx + c\] như hình vẽ.
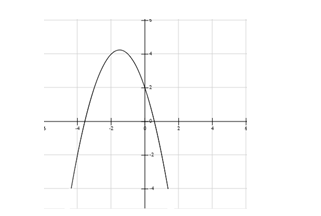
Khẳng định nào sau đây là đúng:
Bề lõm của đồ thị quay xuống dưới nên hệ số a < 0.
Giao điểm của đồ thị hàm số với trục tung nằm trên trục có tung độ dương nên c >0
Hoành độ đỉnh \[x = - \frac{b}{{2a}} < 0\] Mà a < 0 nên b < 0.
Đáp án cần chọn là: D
Câu 2:
Xác định Parabol (P):\[y = a{x^2} + bx + 2\;\] biết rằng Parabol đi qua hai điểm M(1;5) và N(2;−2).
Vì \[M,\,\,N \in (P)\] nên tọa độ của hai điểm M, N phải thỏa mãn phương trình của (P).
Do đó, ta có hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{5 = a + b + 2}\\{ - 2 = 4a + 2b + 2}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = - 5}\\{b = 8}\end{array}} \right.\)
Vậy phương trình của (P)là:\[y = - 5{x^2} + 8x + 2\]
Đáp án cần chọn là: A
Câu 3:
Xác định Parabol (P):\[y = a{x^2} + bx - 5\] biết rằng Parabol đi qua điểm A(3;−4) và có trục đối xứng x = −\(\frac{3}{2}\).
(P) đi qua điểm A(3;−4) nên \[ - 4 = 9a + 3b - 5 \Leftrightarrow 9a + 3b = 1\].
Trục đối xứng \[x = - \frac{b}{{2a}} = - \frac{3}{2} \Leftrightarrow b = 3a\]
Suy ra hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{9a + 3b = 1}\\{3a - b = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = \frac{1}{{18}}}\\{b = \frac{1}{6}}\end{array}} \right.\)
Vậy phương trình của (P)là:\[y = \frac{1}{{18}}{x^2} + \frac{1}{6}x - 5\]
Đáp án cần chọn là: A
Câu 4:
Xác định Parabol (P):\[y = a{x^2} + bx + 3\;\] biết rằng Parabol có đỉnh I(3;−2).
Ta có đỉnh của (P)có tọa độ
\(\left\{ {\begin{array}{*{20}{c}}{x = - \frac{b}{{2a}} = 3}\\{y = 9a + 3b + 3 = - 2}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{6a + b = 0}\\{9a + 3b = - 5}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = \frac{5}{9}}\\{b = - \frac{{10}}{3}}\end{array}} \right.\)
Suy ra phương trình của Parabol (P)là:\[y = \frac{5}{9}{x^2} - \frac{{10}}{3}x + 3\]
Đáp án cần chọn là: D
Câu 5:
Viết phương trình của Parabol (P) biết rằng (P) đi qua các điểm A(0;2),B(−2;5),C(3;8)
Phương trình (P) có dạng \[y = a{x^2} + bx + c\,\,\,\,\left( {a \ne 0} \right)\]
Ba điểm A,B,C thuộc (P) nên tọa độ của chúng phải thỏa mãn phương trình (P)
Do đó, ta có hệ phương trình\(\left\{ {\begin{array}{*{20}{c}}{2 = a{{.0}^2} + b.0 + c}\\{5 = a.{{( - 2)}^2} + b.( - 2) + c}\\{8 = a{{.3}^2} + b.3 + c}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = \frac{7}{{10}}}\\{b = - \frac{1}{{10}}}\\{c = 2}\end{array}} \right.\)
Suy ra phương trình của (P) là: \[y = \frac{7}{{10}}{x^2} - \frac{1}{{10}}x + 2\]
Đáp án cần chọn là: B
Câu 6:
Tìm các giá trị của tham số m để phương trình \[2{x^2} - 2x + 1 - m = 0\;\]có hai nghiệm phân biệt
\[2{x^2} - 2x + 1 - m = 0 \Leftrightarrow 2{x^2} - 2x = m - 1\]
Số nghiệm của phương trình đã cho bằng số giao điểm của Parabol
\[\left( P \right):\,\,y = 2{x^2} - 2x\] và đường thẳng \[y = m - 1\]có tính chất song song với trục hoành.
Parabol (P) có tọa độ đỉnh \[\left( { - \frac{b}{{2a}}; - \frac{{\rm{\Delta }}}{{4a}}} \right) = \left( {\frac{1}{2}; - \frac{1}{2}} \right)\]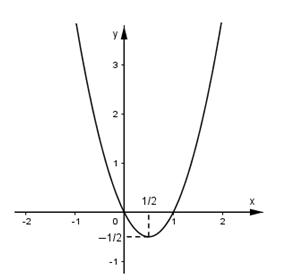
Dựa trên đồ thị ta thấy phương trình đã cho có hai nghiệm khi và chỉ khi
\[m - 1 >- \frac{1}{2} \Leftrightarrow m >\frac{1}{2}\]
Đáp án cần chọn là: A
Câu 7:
Tìm các giá trị thực của tham số m để phương trình \[\left| {{x^2} - 3x + 2} \right| = m\;\] có bốn nghiệm thực phân biệt.
Số nghiệm của phương trình đã cho bằng số giao điểm của đồ thị hàm số
\[y = \left| {{x^2} - 3x + 2} \right|\]với đường thẳng y = m có tính chất song song với trục hoành.
Ta có \[y = \mid {x^2} - 3x + 2\mid = \left\{ {\begin{array}{*{20}{c}}{{x^2} - 3x + 2({x^2} - 3x + 2 \ge 0)}\\{ - {x^2} + 3x - 2({x^2} - 3x + 2 < 0)}\end{array}} \right.\]
Đồ thị hàm số \[y = \left| {{x^2} - 3x + 2} \right|\]được vẽ như sau:
+ Vẽ đồ thị hàm số \[y = {x^2} - 3x + 2\]+ Lấy đối xứng phần đồ thị phía dưới trục hoành qua trục hoành và xóa phần đồ thị dưới trục hoành đi.
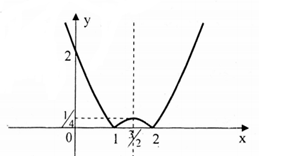
Dựa trên đồ thị ta thấy phương trình đã cho có 4 nghiệm phân biệt khi và chỉ khi \[0 < m < \frac{1}{4}\]
Đáp án cần chọn là: B
Câu 8:
Tìm các giá trị của tham số m để phương trình \[\frac{1}{2}{x^2} - 4\left| x \right| + 3 = {m^2}\] có 3 nghiệm thực phân biệt.
Số nghiệm của phương trình đã cho bằng số giao điểm của đồ thị hàm số
\[y = \frac{1}{2}{x^2} - 4\left| x \right| + 3 = \left\{ {\begin{array}{*{20}{c}}{\frac{1}{2}{x^2} - 4x + 3(x \ge 0)}\\{\frac{1}{2}{x^2} + 4x + 3(x < 0)}\end{array}} \right.\]và đường thẳng \[y = {m^2}\]có tính chất song song với trục hoành.
Đồ thị hàm số \[y = \frac{1}{2}{x^2} - 4\left| x \right| + 3\]được vẽ như sau :
+ Vẽ hai đồ thị hàm số trên cùng một hệ trục tọa độ.
+ Giữ nguyên nhánh bên phải trục tung của đồ thị hàm \[y = \frac{1}{2}{x^2} - 4x + 3\] và xóa nhánh bên trái trục tung.
+ Giữ nguyên nhánh bên trái trục tung của đồ thị hàm số \[y = \frac{1}{2}{x^2} + 4x + 3\] và xóa nhánh bên phải trục tung của đồ thị hàm số đó.
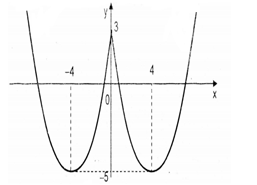
Dựa trên đồ thị ta thấy phương trình đã cho có 3 nghiệm phân biệt khi và chỉ khi
\[{m^2} = 3 \Leftrightarrow m = \pm \sqrt 3 \]
Đáp án cần chọn là: C
Câu 9:
Tìm các giá trị của m để phương trình \[{x^2} - 2x + \sqrt {4{x^2} - 12x + 9} = m\] có nghiệm duy nhất.
Số nghiệm của phương trình đã cho bằng số giao điểm của đồ thị hàm số
\[y = {x^2} - 2x + \left| {2x - 3} \right|\]và đường thẳng y = m có tính chất song song với trục hoành.
Đồ thị hàm số \[y = {x^2} - 2x + |2x - 3|\]
\( = \left\{ {\begin{array}{*{20}{c}}{{x^2} - 2x + 2x - 3 = {x^2} - 3({P_1})\,khi\,x \ge \frac{3}{2}}\\{{x^2} - 2x - 2x + 3 = {x^2} - 4x + 3({P_2})\,khi\,x < \frac{3}{2}}\end{array}} \right.\)
được vẽ như sau:
+ Vẽ lần lượt hai đồ thị hàm số trên cùng một hệ trục tọa độ
+ Xóa đi nhánh bên trái điểm \[x = \frac{3}{2}\] của đồ thị hàm số \[y = {x^2} - 3\]
+ Xóa đi nhánh bên phải điểm \[x = \frac{3}{2}\]của đồ thị hàm số \[y = {x^2} - 4x + 3\]![Tìm các giá trị của m để phương trình \[{x^2} - 2x + \sqrt {4{x^2} - 12x + 9} = m\] có nghiệm duy nhất. (ảnh 1)](https://video.vietjack.com/upload2/images/1652771117/1652771317-image5.png)
Tọa độ giao điểm của đồ thị hàm số (P1) và (P2) là \[\left( {\frac{3}{2}; - \frac{3}{4}} \right)\]
Dựa trên đồ thị ta thấy phương trình đã cho có nghiệm duy nhất khi và chỉ khi \[m = - \frac{3}{4}\]
Đáp án cần chọn là: C
Câu 10:
Cho phương trình của (P):\[y = a{x^2} + bx + c\left( {a \ne 0} \right)\] biết rằng hàm số có giá trị lớn nhất bằng 1 và đồ thị hàm số đi qua các điểm A(2;0), B(−2;−8) Tình tổng \[{a^2} + {b^2} + {c^2}\]
Dễ thấy rằng đồ thị của (P) có đỉnh đặt trên đường thẳng y = 1 và hệ số m < 0..
Do đó, phương trình của (P) có dạng \[y = m{\left( {x - u} \right)^2} + 1\,\,(m < 0)\](P) đi qua các điểm A(2;0), B(−2;−8) nên có hệ phương trình
\(\left\{ {\begin{array}{*{20}{c}}{m{{(2 - u)}^2} + 1 = 0}\\{m{{( - 2 - u)}^2} + 1 = - 8}\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{c}}{m = - \frac{1}{{{{(2 - u)}^2}}}}\\{m = - \frac{9}{{{{( - 2 - u)}^2}}}}\end{array}} \right. \Rightarrow \Rightarrow - \frac{1}{{{{\left( {2 - u} \right)}^2}}} = - \frac{9}{{{{\left( { - 2 - u} \right)}^2}}}\)
\[ \Rightarrow {\left( {u + 2} \right)^2} = 9{\left( {2 - u} \right)^2} \Leftrightarrow 8{u^2} - 40u + 32 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{u = 1}\\{u = 4}\end{array}} \right.\]
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\left\{ {\begin{array}{*{20}{c}}{u = 1}\\{m = - 1\left( {tm} \right)}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{c}}{u = 4}\\{m = - \frac{1}{4}\left( {tm} \right)}\end{array}} \right.}\end{array}} \right.\)
Từ đây có hai phương trình (P) thỏa mãn là\[y = - {x^2} + 2x,\,\,\,y = - \frac{1}{4}{x^2} + 2x - 3\]
Suy ra \[{a^2} + {b^2} + {c^2} = 5\] hoặc \[{a^2} + {b^2} + {c^2} = \frac{{209}}{{16}}\]
Đáp án cần chọn là: D
Câu 11:
Biết đồ thị hàm số (P):\[y = {x^2} - ({m^2} + 1)x - 1\] cắt trục hoành tại hai điểm phân biệt có hoành độ x1,x2. Tìm giá trị của tham số mm để biểu thức \[T = {x_1} + {x_2}\;\] đạt giá trị nhỏ nhất.
Dễ thấy rằng phương trình hoành độ giao điểm có hai nghiệm phân biệt vì a.c= 1.(−1) < 0 và hai giao điểm có cùng tung độ và có hoành độ đối xứng với nhau qua trục đối xứng \[x = \frac{{{m^2} + 1}}{2}\]
Từ đây suy ra \[T = {x_1} + {x_2} = {m^2} + 1 \ge 1\,\,\forall m\]
Suy ra \[{T_{\min }} = {\left( {{x_1} + {x_2}} \right)_{\min }} = 1\] và đạt được khi m = 0 .
Đáp án cần chọn là: C
Câu 12:
Tìm các giá trị của tham số mm để phương trình \[{x^2} - 2(m + 1)x + 1 = 0\;\] có hai nghiệm phân biệt trong đó có đúng một nghiệm thuộc khoảng (0;1).
Có: \[{\rm{\Delta '}} = {\left( {m + 1} \right)^2} - 1 = m\left( {m + 2} \right)\]
Phương trình có hai nghiệm phân biệt ⇔\[m(m + 2) >0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m >0}\\{m < - 2}\end{array}} \right.\]Khi đó dạng đồ thị hàm số \[y = {x^2} - 2\left( {m + 1} \right)x + 1\] chỉ có thể là:
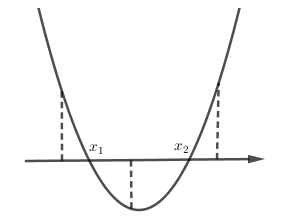
Quan sát đồ thị ta thấy:
Yêu cầu bài toán tương đương \[f\left( 0 \right).f\left( 1 \right) < 0 \Leftrightarrow 1.\left( { - 2m} \right) < 0 \Leftrightarrow m >0\]</>
Kết hợp điều kiện có hai nghiệm phân biệt ta được m >0
Đáp án cần chọn là: A
Câu 13:
Tìm các giá trị của tham số m để \[2{x^2} - 2(m + 1)x + {m^2} - 2m + 4 \ge 0(\forall x)\]
Yêu cầu bài toán tương đương tìm giá trị của m để đồ thị hàm số
\[\left( P \right):y = 2{x^2} - 2\left( {m + 1} \right)x + {m^2} - 2m + 4\] luôn nằm phía trên trên trục hoành.
Suy ra với giá trị x0 thì giá trị nhỏ nhất của hàm số đã cho lớn hơn hoặc bằng 0.
Parabol có hệ số a = 2 >0 nên có bề lõm hướng lên trên đạt GTNN tại đỉnh parabol \[x = \frac{{m + 1}}{2}\]
Điều này tương đương với \[y\left( {\frac{{m + 1}}{2}} \right) \ge 0\]
\[ \Leftrightarrow 2{\left( {\frac{{m + 1}}{2}} \right)^2} - 2\left( {m + 1} \right)\left( {\frac{{m + 1}}{2}} \right) + {m^2} - 2m + 4 \ge 0\]
\[ \Leftrightarrow \frac{1}{2}({m^2} - 6m + 7) \ge 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m \ge 3 + \sqrt 2 }\\{m \le 3 - \sqrt 2 }\end{array}} \right.\]
Đáp án cần chọn là: C
Câu 14:
Tìm giá trị nhỏ nhất của hàm số f(x) biết rằng \[f(x + 2) = {x^2} - 3x + 2\;\] trên \(\mathbb{R}\)
Đặt \[t = x + 2 \Rightarrow x = t - 2\] từ đẳng thức trên ta suy ra
\[f\left( t \right) = {\left( {t - 2} \right)^2} - 3\left( {t - 2} \right) + 2 = {t^2} - 7t + 12\]
Suy ra \[f\left( x \right) = {x^2} - 7x + 12\]
\[ = {x^2} - 2.\frac{7}{2}x + {\left( {\frac{7}{2}} \right)^2} - \frac{1}{4}\]
\[ = {\left( {x - \frac{7}{2}} \right)^2} - \frac{1}{4} \ge - \frac{1}{4}\forall x \in R\]
Vậy \[Minf\left( x \right) = - \frac{1}{4}\] khi \[x = \frac{7}{2}\]
Đáp án cần chọn là: A
Câu 15:
Cho hàm số \[f(x) = {x^2} + 2x - 3\].
Xét các mệnh đề sau:
i) \[f(x - 1) = {x^2} - 4\]
ii) Hàm số đã cho đồng biến trên \[\left( { - 1; + \infty } \right)\]
iii) Giá trị nhỏ nhất của hàm số là một số âm.
iv) Phương trình \[f(x) = m\;\] có nghiệm khi \[m \ge - 4\]
Số mệnh đề đúng là:
Ta có \[f\left( {x - 1} \right) = {\left( {x - 1} \right)^2} + 2\left( {x - 1} \right) - 3 = {x^2} - 4\]
Với trục đối xứng \[x = - \frac{b}{{2a}} = - 1\] và hệ số \[a = 1 >0\] thì hàm số đồng biến trên \[\left( { - 1;\,\, + \infty } \right)\]
Biến đối \[f\left( x \right) = {x^2} + 2x - 3 = {\left( {x + 1} \right)^2} - 4 \ge - 4\] ⇒ GTNN của hàm số là −4 < 0
Dễ thấy \[f\left( x \right) = m \Leftrightarrow {\left( {x + 1} \right)^2} = m + 4\] nên để phương trình có nghiệm thì \[m + 4 \ge 0 \Leftrightarrow m \ge - 4\]
Đáp án cần chọn là: D
Câu 16:
Tìm các giá trị của m để hàm số \[y = {x^2} + mx + 5\;\] luôn đồng biến trên \[\left( {1; + \infty } \right)\]
Trục đối xứng \[x = - \frac{b}{{2a}} = - \frac{m}{2}\]
Với hệ số a = 1 >0 thì hàm số đã cho đồng biến trên \[\left( { - \frac{m}{2};\,\, + \infty } \right)\]
Vậy để hàm số luôn đồng biến trên \[\left( {1;\,\, + \infty } \right)\] thì \[ - \frac{m}{2} \le 1 \Leftrightarrow m \ge - 2\]
Đáp án cần chọn là: B
Câu 17:
Tìm giá trị của m để hàm số \[y = - {x^2} + 2x + m - 5\] đạt giá trị lớn nhất bằng 6
Hàm số đã cho đạt giá trị lớn nhất tại \[x = - \frac{b}{{2a}} = 1\] Khi đó \[\max y = f\left( 1 \right) = m - 4\]
Để \[\max y = 6\] thì \[m - 4 = 6 \Leftrightarrow m = 10\]
Đáp án cần chọn là: B
Câu 18:
Tìm giá trị của m để đồ thị hàm số \[y = {x^2} - 2x + m - 1\] cắt trục hoành tại hai điểm phân biệt có hoành độ dương.
Xét phương trình hoành độ giao điểm \[{x^2} - 2x + m - 1 = 0\,\,\left( * \right)\]
Để đồ thị hàm số \[y = {x^2} - 2x + m - 1\] cắt trục hoành tại hai điểm phân biệt có hoành độ dương thì phương trình (*) có 2 nghiệm dương phân biệt.
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\Delta \prime >0}\\{S >0}\\{P >0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{1 - m + 1 >0}\\{2 >0}\\{m - 1 >0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{m < 2}\\{m >1}\end{array}} \right. \Leftrightarrow 1 < m < 2\)
Đáp án cần chọn là: C
Câu 19:
Tìm điểm A cố định mà họ đồ thị hàm số \[y = {x^2} + (2 - m)x + 3m\,\,\,\,\,\,\,\,\,\,({P_m})\;\] luôn đi qua.
Điểm\[A\left( {{x_0};\,\,{y_0}} \right)\] là điểm cố định của họ (Pm) khi và chỉ khi
\[{y_0} = {x_0}^2 + (2 - m){x_0} + 3m \Leftrightarrow x_0^2 + 2{x_0} - {y_0} - m({x_0} - 3) = 0,\forall m\]
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x_0^2 + 2{x_0} - {y_0} = 0}\\{{x_0} - 3 = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{x_0} = 3}\\{{y_0} = 15}\end{array}} \right.\)
Suy ra A(3;15).
Đáp án cần chọn là: A
Câu 20:
Tìm giá trị nhỏ nhất của biểu thức \[P = 3\left( {\frac{{{a^2}}}{{{b^2}}} + \frac{{{b^2}}}{{{a^2}}}} \right) - 8\left( {\frac{a}{b} + \frac{b}{a}} \right)\].
Ta có :
\[{\left( {\frac{a}{b} + \frac{b}{a}} \right)^2} = \frac{{{a^2}}}{{{b^2}}} + 2\frac{a}{b}.\frac{b}{a} + \frac{{{b^2}}}{{{a^2}}} = \frac{{{a^2}}}{{{b^2}}} + \frac{{{b^2}}}{{{a^2}}} + 2 \Rightarrow \frac{{{a^2}}}{{{b^2}}} + \frac{{{b^2}}}{{{a^2}}} = {\left( {\frac{a}{b} + \frac{b}{a}} \right)^2} - 2\]
Biến đổi biểu thức P về dạng
\[P = 3{\left( {\frac{a}{b} + \frac{b}{a}} \right)^2} - 6 - 8\left( {\frac{a}{b} + \frac{b}{a}} \right) = 3{\left( {\frac{a}{b} + \frac{b}{a}} \right)^2} - 8\left( {\frac{a}{b} + \frac{b}{a}} \right) - 6\]
Đặt \[t = \frac{a}{b} + \frac{b}{a} \Rightarrow {t^2} = {\left( {\frac{a}{b} + \frac{b}{a}} \right)^2}\]
Áp dụng bất đẳng thức \[{\left( {x + y} \right)^2} \ge 4xy\,\,\forall x,y\] với hai số \[\frac{a}{b}\] và \[\frac{b}{a}\] ta có :
\[{t^2} = {(\frac{a}{b} + \frac{b}{a})^2} \ge 4\frac{a}{b}.\frac{b}{a} = 4 \Leftrightarrow |t| \ge 2 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{t \ge 2}\\{t \le - 2}\end{array}} \right.\]
Biểu thức P trở thành \[P = 3{t^2} - 8t - 6\]Trục đối xứng \[x = - \frac{b}{{2a}} = \frac{4}{3}\] và hệ số \[a = 3 >0.\]
Suy ra hàm số \[f\left( t \right) = 3{t^2} - 8t - 6\] nghịch biến trên khoảng \[\left( { - \infty ;\frac{4}{3}} \right)\] và đồng biến trên khoảng \[\left( {\frac{4}{3}; + \infty } \right)\]BBT :
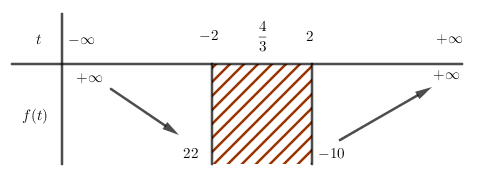
Từ đây suy ra hàm số f(t) đạt giá trị nhỏ nhất tại t = 2
Ta có f(2 )= −10.
Vậy minP = minf(t) = −10.
Đáp án cần chọn là: D
Câu 21:
Một chiếc cổng parabol dạng \[y = - 12{x^2}\;\] có chiều rộng d = 8m. Hãy tính chiều cao h của cổng ?
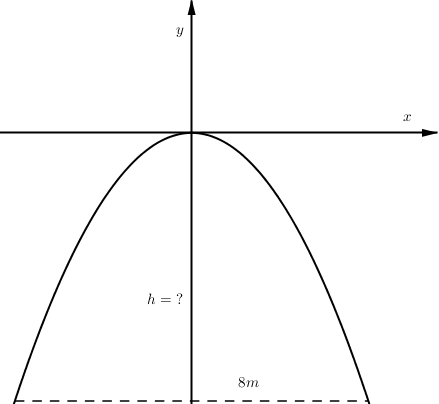
Khoảng cách từ chân cổng đến trục đối xứng Oy là\[\frac{8}{2} = 4\] Hoành độ 2 chân cổng là −4 và 4.
Tung độ chân cổng là \[y = \frac{{ - 1}}{2}{.4^2} = - 8\]
Chiều cao của cổng là \[\left| { - 8} \right| = 8m\]
Đáp án cần chọn là: A
Câu 22:
Một cái cổng hình parabol có dạng \[y = - \frac{1}{2}{x^2}\;\] có chiều rộng d = 4m.
Tính chiều cao h của cổng (xem hình minh họa)
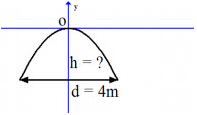
Bước 1:
Gọi hai điểm chân cổng là \[A\left( {{x_A};{y_A}} \right)\] và \[B\left( {{x_B};{y_B}} \right)\] thì ta có \[{y_A} = {y_B}\] và \[\left| {{x_A}} \right| = \left| {{x_B}} \right|.\]
Vì d = 4 nên \[\left| {{x_A}} \right| = \left| {{x_B}} \right| = 2.\]
Bước 2: Tính h
Vậy \[h = \left| {{y_A}} \right| = \left| { - \frac{1}{2}x_A^2} \right| = \left| { - \frac{1}{2}{{.2}^2}} \right| = 2\,\left( m \right).\]
