Cho aa là số thực dương, khác 1 và thỏa mãn \[\frac{1}{2}({a^\alpha } + {a^{ - \alpha }}) = 1\;\]. Tìm \[\alpha \]
A.\[\alpha = 1\]
B. \[\alpha \in R\]
C. \[\alpha = 0\]
D. \[\alpha = - 1\]
Giải bởi qa.haylamdo.com
Áp dụng bất đẳng thức Cauchy ta có .
Dấu "=" xảy ra khi \[{a^\alpha } = {a^{ - \alpha }}\]. Điều này dẫn đến \[\alpha = - \alpha \Rightarrow \alpha = 0\]
Đáp án cần chọn là: C
Phương trình \[{2^{23{x^3}}}{.2^x} - {1024^{{x^2}}} + 23{x^3} = 10{x^2} - x\] có tổng các nghiệm gần nhất với số nào dưới đây:
Có bao nhiêu giá trị nguyên dương của tham số m để phương trình \[{16^x} - {2.12^x} + \left( {m - 2} \right){.9^x} = 0\]có nghiệm dương?
Cho hàm số y=f(x) có bảng biến thiên như sau
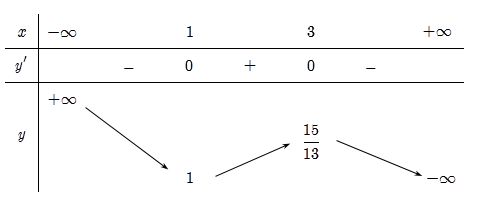
Biết f(0)=76, giá trị lớn nhất của mm để phương trình \[{e^{2{f^3}\left( x \right) - \frac{{13}}{2}{f^2}\left( x \right) + 7f\left( x \right) + \frac{3}{2}}} = m\] có nghiệm trên đoạn \[\left[ {0;2} \right]\;\]là
Tìm nghiệm của phương trình \[\frac{{{3^{2x - 6}}}}{{27}} = {\left( {\frac{1}{3}} \right)^x}.\]
Biết phương trình \[{9^x} - {2^{x + \frac{1}{2}}} = {2^{x + \frac{3}{2}}} - {3^{2x - 1}}\]có nghiệm là a. Tính giá trị của biểu thức \[P = a + \frac{1}{2}lo{g_{\frac{9}{2}}}2\;\].
Tìm nghiệm của phương trình \[{9^{\sqrt {x - 1} }} = {e^{\ln 81}}\]
Tìm giá trị của a để phương trình \[{(2 + \sqrt 3 )^x} + (1 - a){(2 - \sqrt 3 )^x} - 4 = 0\;\]có 2 nghiệm phân biệt thỏa mãn:\[{x_1} - {x_2} = lo{g_{2 + \sqrt 3 }}3\], ta có a thuộc khoảng:
Tìm tập hợp tất cả các nghiệm của phương trình \[{2^{{x^2} + x - 1}} = \frac{1}{2}\].
Tìm tham số m để tổng các nghiệm của phương trình sau đạt giá trị nhỏ nhất \[1 + \left[ {2{x^2} - m\left( {m + 1} \right)x - 2} \right]{.2^{1 + mx - {x^2}}} = \left( {{x^2} - mx - 1} \right){.2^{mx\left( {1 - m} \right)}} + {x^2} - {m^2}x\].
Tìm tập nghiệm S của phương trình: \[{4^{x + 1}} + {4^{x - 1}} = 272\]
Phương trình \[x({2^{x - 1}} + 4) = {2^{x + 1}} + {x^2}\]có tổng các nghiệm bằng
Tìm m để phương trình \[{4^x} - \;{2^{x\; + \;3}} + \;3\; = \;m\;\] có đúng 2 nghiệm \[x \in \left( {1;3} \right)\;\].
