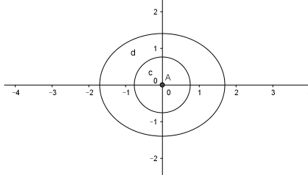
Người ta cần trồng hoa tại phần đắt nằm phía ngoài đường tròn tâm gốc tọa độ O , bán kính bằng 1√2và phía trong của Elip có độ dài trục lớn bằng 2√2và độ dài trục nhỏ bằng 2 (như hình vẽ bên). Trong mỗi một đơn vị diện tích cần bón 100(2√2−1)πkg phân hữu cơ. Hỏi cần sử dụng bao nhiêu kg phân hữu cơ để bón cho hoa?
A.30kg
B.40kg
C.50kg
D.45kg
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Phương trình elip:x2(√2)2+y21=1
Ta có :y=√1−x22 (nửa trên của elip)
Diện tích của elip là: S=4∫√20√1−x22dx
Đặtx=√2cosa⇒1−x22=sin2a
Suy ra:dx=−√2sinada
Đổi cậnx=√2⇒a=0,x=0thìa=π2
S1=0∫π2−√2sin2ada=√220∫π2(cos2a−1)da
=√22(12sin2a−a)|π20=√2π4
⇒S=4S1=√2π
Diện tích hình tròn là :S′=πR2=π.12=12π
Diện tích trồng hoa: Sb=π(√2−12)
Số kg phân bón là :100(2√2−1)π.(√2−12)π=50kg
Đáp án cần chọn là: C
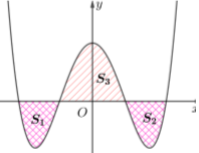
Cho hàm số y=x4−3x2+m có đồ thị là (Cm) (m là tham số thực). Giả sử (Cm) cắt trục Ox tại 4 điểm phân biệt. Gọi S1,S2 là diện tích của hai hình phẳng nằm dưới trục Ox và S3 là diện tích của hình phẳng nằm trên trục Ox được tạo bởi (Cm) với trục Ox. Biết rằng tồn tại duy nhất giá trị m=ab (với a,b∈N∗ và tối giản) để S1+S2=S3. Giá trị của 2a−b bằng:
Tính diện tích S của hình phẳng giới hạn bởi đồ thị của hai hàm số y=x2−4 và y=x−4
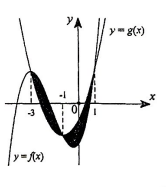
Cho hai hàm số f(x)=mx3+nx2+px−52(m,n,p∈R)vàg(x)=x2+3x−1 có đồ thị cắt nhau tại ba điểm có hoành độ lần lượt là −3;−1;1( tham khảo hình vẽ bên). Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số f(x)và g(x) bằng
Công thức tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y=f(x),y=g(x) và hai đường thẳng x=a,x=b(a<b) là:
Cho parabol (P):y=x2+1và đường thẳng (d):y=mx+2. Biết rằng tồn tại m để diện tích hình phẳng giới hạn bới (P) và (d) đạt giá trị nhỏ nhất, tính diện tích nhỏ nhất đó.
Gọi S là diện tích hình phẳng giới hạn bởi các đường y=x3,y=2−xvà y = 0. Mệnh đề nào sau đây là đúng?
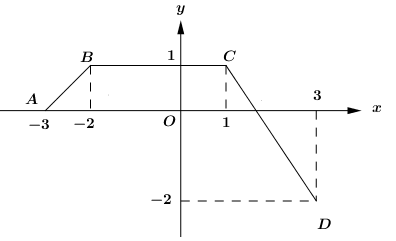
Cho hàm số f(x) có đồ thị trên đoạn [−3;3]là đường gấp khúc ABCD như hình vẽ.
Tính 3∫−3f(x)dx
Cho hai hàm số f(x)=−x và g(x)=ex. Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số y=f(x),y=g(x) và hai đường thẳng x=0,x=e là:
Tìm diện tích hình phẳng giới hạn bởi các đường y=(x−1)ex, trục hoành, đường thẳng x=0 và x=1
Công thức tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y=f(x)=x2−1, trục hoành và hai đường thẳng x=−1;x=−3 là:
Công thức tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y=f(x), đường thẳng y=0 và hai đường thẳng x=a,x=b(a<b) là:
Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình vẽ.
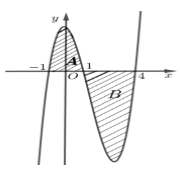
Diện tích hai phần A và B lần lượt là 163 và 634. Tính 32∫−1f(2x+1)dx
Cho hình vuông ABCD tâm O, độ dài cạnh là 4cm. Đường cong BOC là một phần của parabol đỉnh O chia hình vuông thành hai hình phẳng có diện tích lần lượt là S1 và S2 (tham khảo hình vẽ).
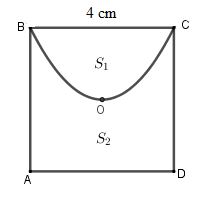
Tỉ số S1S2 bằng:
Diện tích hình phẳng giới hạn bởi nửa đường tròn x2+y2=2,y>0 và parabol y=x2 bằng:
Vòm cửa lớn của một trung tâm văn hóa có hình parabol. Gắn parabol vào hệ trục Oxy thì nó có đỉnh (0;8) và cắt trục hoành tại 2 điểm phân biệt, trong đó có 1 điểm là (−4;0). Người ta dự định lắp vào cửa kính cho vòm cửa này. Hãy tính diện tích mặt kính cần lắp vào.