Đề thi THPT QG - 2021 - mã 101
Cho hàm số f(x)=x3+ax2+bx+c với a,b,c là các số thực. Biết hàm số g(x)=f(x)+f′(x)+f′′(x) có hai giá trị cực trị là −3 và 6. Diện tích hình phẳng giới hạn bởi các đường y=f(x)g(x)+6v\`ay=1 bằng
A.2ln3.
B.ln3.
C.ln18.
D.2ln2.
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
* Xét phương trình hoành độ giao điểm:
f(x)g(x)+6=1⇔f(x)=g(x)+6⇔f(x)−g(x)−6=0
(Chúng ta không cần lo điều kiệng(x)+6≠0 bởi lẽ đồ thị hàm số y=f(x)g(x)+6 khi tương giao với đường thẳngy=1 phải tạo nên một miền kín, và khi số nghiệm của phương trìnhf(x)=g(x)+6 nhiều hơn 2 thì ta mới phải chú ý xem xét lấy cận từ đâu đến đâu, và liệu rằng có phải từxmin chẳng may đồ thị tương giao bị gián đoạn trên đoạn\left[ {{x_{\min }};{x_{\max }}} \right] mà vẫn tạo miền kín. Trên thực tế, bài toán này phương trìnhf\left( x \right) = g\left( x \right) + 6 chỉ có 2 nghiệm (vì là phương trình bậc hai), nên người giải toán không cần quan tâm đến việc gián đoạn hay không, vì việc tồn tại nghiệm hình và hàm số là thuộc phạm trù người ra đề).
Màg\left( x \right) = f\left( x \right) + f'\left( x \right) + f''\left( x \right) \Rightarrow f\left( x \right) - g\left( x \right) = - f'\left( x \right) - f''\left( x \right)
⇒⇒ Phương trình hoành độ giao điểm trở thành:
- f'\left( x \right) - f''\left( x \right) - 6 = 0 \Leftrightarrow f'\left( x \right) + f''\left( x \right) + 6 = 0(1)
Mặt khác:g'\left( x \right) = f'\left( x \right) + f''\left( x \right) + f'''\left( x \right) vàf'''\left( x \right) = 6
\Rightarrow g'\left( x \right) = f'\left( x \right) + f''\left( x \right) + 6
Từ phương trình (1) \Leftrightarrow g'\left( x \right) = 0
Theo giả thiết g(x) có 2 điểm cực trị{x_1},\,\,{x_2} sao cho\left\{ {\begin{array}{*{20}{c}}{g({x_1}) = - 3}\\{g({x_2}) = 6}\end{array}} \right. \Rightarrow g'\left( x \right) = 0 có 2 nghiệm{x_1},\,\,{x_2}
Vậy phương trình hoành độ giao điểm có 2 nghiệm{x_1},\,\,{x_2}
\Rightarrow {S_{\left( H \right)}} = \left| {\int\limits_{{x_1}}^{{x_2}} {\left( {\frac{{f(x)}}{{g(x) + 6}} - 1} \right)dx} } \right|
\begin{array}{l} = \left| {\int\limits_{{x_1}}^{{x_2}} {\frac{{f(x) - g(x) - 6}}{{g(x) + 6}}dx} } \right|\\ = \left| {\int\limits_{{x_1}}^{{x_2}} {\frac{{ - f\prime (x) - f\prime \prime (x) - 6}}{{g(x) + 6}}dx} } \right|\\ = \left| {\int\limits_{{x_1}}^{{x_2}} {\frac{{ - g\prime (x)}}{{g(x) + 6}}dx} } \right|\end{array}
= \left| {\int\limits_{{x_1}}^{{x_2}} {\frac{{g\prime (x)}}{{g(x) + 6}}dx} } \right|
= \left| {\int\limits_{{x_1}}^{{x_2}} {\frac{{d(g(x) + 6)}}{{g(x) + 6}}dx} } \right|
\begin{array}{l} = \mid ln|g(x) + 6||_{{x_1}}^{{x_2}}\mid \\ = |ln|g({x_2}) + 6| - ln|g({x_1}) + 6||\\ = |ln|6 + 6| - ln| - 3 + 6|| = ln12 - ln3 = 2ln2\end{array}
Đáp án cần chọn là: D
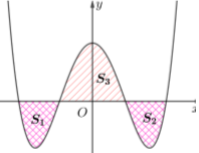
Cho hàm số y = {x^4} - 3{x^2} + m có đồ thị là (Cm) (m là tham số thực). Giả sử (Cm) cắt trục Ox tại 4 điểm phân biệt. Gọi {S_1},{S_2}\; là diện tích của hai hình phẳng nằm dưới trục Ox và S3 là diện tích của hình phẳng nằm trên trục Ox được tạo bởi (Cm) với trục Ox. Biết rằng tồn tại duy nhất giá trị m = \frac{a}{b} (với a,b \in {\mathbb{N}^*}\; và tối giản) để {S_1} + {S_2} = {S_3}. Giá trị của 2a−b bằng:
Tính diện tích S của hình phẳng giới hạn bởi đồ thị của hai hàm số y = {x^2} - 4\; và y = x - 4
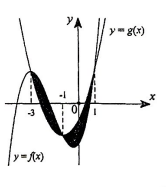
Cho hai hàm số f\left( x \right) = m{x^3} + n{x^2} + px - \frac{5}{2}\left( {m,n,p \in \mathbb{R}} \right)vàg\left( x \right) = {x^2} + 3x - 1 có đồ thị cắt nhau tại ba điểm có hoành độ lần lượt là −3;−1;1( tham khảo hình vẽ bên). Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số f(x)và g(x) bằng
Công thức tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f\left( x \right),y = g\left( x \right) và hai đường thẳng x = a,x = b(a < b)\; là:
Cho parabol \left( P \right):y = {x^2} + 1và đường thẳng (d):y = mx + 2. Biết rằng tồn tại m để diện tích hình phẳng giới hạn bới (P) và (d) đạt giá trị nhỏ nhất, tính diện tích nhỏ nhất đó.
Gọi S là diện tích hình phẳng giới hạn bởi các đường y = {x^3},y = 2 - xvà y = 0. Mệnh đề nào sau đây là đúng?
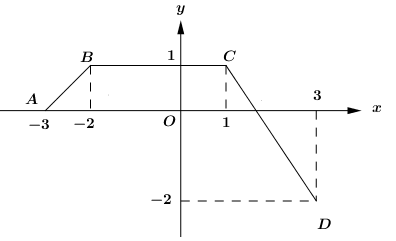
Cho hàm số f(x) có đồ thị trên đoạn \left[ { - 3;3} \right]\;là đường gấp khúc ABCD như hình vẽ.
Tính \mathop \smallint \limits_{ - 3}^3 f\left( x \right)dx
Cho hai hàm số f(x) = - x\; và g(x) = {e^x}. Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số y = f(x),y = g(x)\; và hai đường thẳng x=0,x=e là:
Tìm diện tích hình phẳng giới hạn bởi các đường y = (x - 1){e^x}, trục hoành, đường thẳng x=0 và x=1
Công thức tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f\left( x \right) = {x^2} - 1, trục hoành và hai đường thẳng x=−1;x=−3 là:
Công thức tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y=f(x), đường thẳng y=0 và hai đường thẳng x = a,x = b(a < b) là:
Cho hình vuông ABCD tâm O, độ dài cạnh là 4cm. Đường cong BOC là một phần của parabol đỉnh O chia hình vuông thành hai hình phẳng có diện tích lần lượt là S1 và S2 (tham khảo hình vẽ).
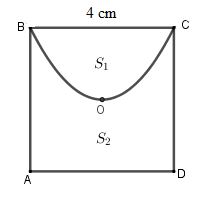
Tỉ số \frac{{{S_1}}}{{{S_2}}} bằng:
Cho hàm số y=f(x) liên tục trên \mathbb{R} và có đồ thị như hình vẽ.
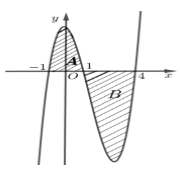
Diện tích hai phần A và B lần lượt là \frac{{16}}{3} và \frac{{63}}{4}. Tính \mathop \smallint \limits_{ - 1}^{\frac{3}{2}} f\left( {2x + 1} \right)dx
Diện tích hình phẳng giới hạn bởi nửa đường tròn {x^2} + {y^2} = 2,y > 0 và parabol y = {x^2}\; bằng:
Vòm cửa lớn của một trung tâm văn hóa có hình parabol. Gắn parabol vào hệ trục Oxy thì nó có đỉnh (0;8) và cắt trục hoành tại 2 điểm phân biệt, trong đó có 1 điểm là (−4;0). Người ta dự định lắp vào cửa kính cho vòm cửa này. Hãy tính diện tích mặt kính cần lắp vào.