Chứng minh rằng a2 + b2 + 4 ≥ ab + 2(a + b) với mọi a, b.
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Hướng dẫn giải
Xét I = a2 + b2 + 4 - ab - 2(a + b)
Û 2I = 2a2 + 2b2 + 8 - 2ab - 4(a + b) (nhân 2 vế của phương trình với 2)
Û 2I = 2a2 + 2b2 + 8 - 2ab - 4a - 4b
Û 2I = (a2 - 2ab + 2b2) + (a2 - 4a + 4) + (b2 - 4b + 4)
Û 2I = (a - b)2 + (a - 2)2 + (b - 2)2 ³ 0 "a, b
Þ I ³ 0 "a, b
Từ đó suy ra a2 + b2 + 4 - ab - 2(a + b) ³ 0 "a, b
Vậy a2 + b2 + 4 ≥ ab + 2(a + b) với mọi a, b.
Cho DABC vuông tại A, có AB = 3cm, BC = 5cm. Tia phân giác của cắt BC tại E thì bằng
d) Tìm vị trí của điểm E trên cạnh AB để tam giác HEF có diện tích nhỏ nhất.
Cho ∆ABC ᔕ ∆MNP với tỉ số đồng dạng là . Khi đó tỉ số chu vi của DABC và DMNP là
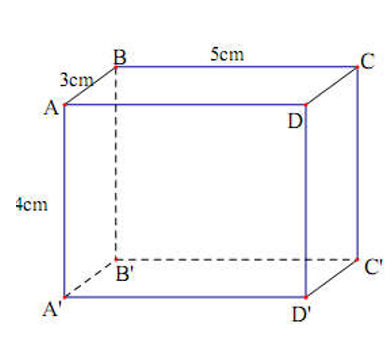
Hình hộp chữ nhật ABCD.A’B’C’D’ có AB = 3cm; BC = 5cm; AA’ = 4cm (hình vẽ). Khi đó thể tích của hình hộp chữ nhật là
Cửa hàng đồng giá 50 000 đồng một món, có chương trình giảm giá 10% cho một món hàng. Nếu khách hàng mua 3 món trở lên thì từ món thứ 3 trở đi khách hàng chỉ phải trả 70% giá đang bán.
a) Tính số tiền một khách hàng phải trả khi mua 8 món hàng.
c) Gọi E là điểm tùy ý trên cạnh AB, đường thẳng qua H và vuông góc với HE cắt cạnh AC tại F. Chứng minh AE.CH = AH.FC.