Cho nhọn . Kẻ đường cao Gọi là trung điểm của là điểm đối xứng của qua
Gọi là giao điểm của và Chứng minh:
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Phương pháp:
Sử dụng các mối quan hệ vuông góc và song song.
Cách giải:
Gọi là giao điểm của và Chứng minh:
Ta có: là hình chữ nhật (cmt) (tính chất hình chữ nhật)
Mà
là hình bình hành. (dhnb)
với là trung điểm của và
Xét ta có:
lần lượt là trung điểm của và
là đường trung bình của (định nghĩa).
hay (dpcm).
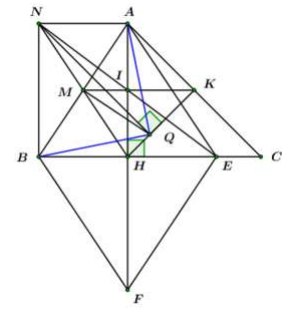
Cho nhọn . Kẻ đường cao Gọi là trung điểm của là điểm đối xứng của qua
Chứng minh: Tứ giác là hình chữ nhật.
Cho đa thức và đa thức
Tìm đa thức thương và đa thức dư của phép chia đa thức cho đa thức
Cho nhọn . Kẻ đường cao Gọi là trung điểm của là điểm đối xứng của qua
Trên tia đối của tia lấy điểm sao cho là trung điểm của Gọi là điểm đối xứng với qua Chứng minh: Tứ giác là hình thoi.
Cho đa thức và đa thức
Tìm các giá trị nguyên của sao cho giá trị của đa thức chia hết cho giá trị của đa thức
Cho nhọn . Kẻ đường cao Gọi là trung điểm của là điểm đối xứng của qua
Đường thẳng cắt tại Kẻ vuông góc với tại Chứng minh: