14 câu hỏi trắc nghiệm thuộc Bộ 14 đề thi Học kì 1 Toán 8 có đáp án - Đề 6

Câu 1:

Thực hiện phép tính:

$2 x (x + 3) + (1 - x) (2 x - 1)$

Xem đáp án

Phương pháp: Sử dụng quy tắc nhân đơn, đa thức với đa thức và bảy hằng đẳng thức đáng nhớ:

+) Quy tắc: $A (B + C) = A B + A C$

$(A + B) (C + D) = A B + A C + B C + B D$

+) Bảy hằng đẳng thức đáng nhớ.

Cách giải:

$2 x (x + 3) + (1 - x) (2 x - 1)$

$2 x^{2} + 6 x + 2 x - 1 - 2 x^{2} + x$

$= 9 x - 1$

Câu 2:

Thực hiện phép tính:

$(x + 2) (x - 2) + (3 - x) (x + 1)$

Xem đáp án

Phương pháp: Sử dụng quy tắc nhân đơn, đa thức với đa thức và bảy hằng đẳng thức đáng nhớ:

+) Quy tắc: $A (B + C) = A B + A C$

$(A + B) (C + D) = A B + A C + B C + B D$

+) Bảy hằng đẳng thức đáng nhớ.

Cách giải:

$(x + 2) (x - 2) + (3 - x) (x + 1)$

$= x^{2} - 4 + 3 x + 3 - x^{2} - x$

$= 2 x - 1.$

Câu 3:

Thực hiện phép tính:

$\frac{x}{x - 3} + \frac{9 - 6 x}{x^{2} - 3 x}$

Xem đáp án

Phương pháp: Sử dụng quy tắc nhân đơn, đa thức với đa thức và bảy hằng đẳng thức đáng nhớ:

+) Quy tắc: $A (B + C) = A B + A C$

$(A + B) (C + D) = A B + A C + B C + B D$

+) Bảy hằng đẳng thức đáng nhớ.

Cách giải:

$\frac{x}{x - 3} + \frac{9 - 6 x}{x^{2} - 3 x}$ $(D K : x \neq 0, x \neq 3)$

$= \frac{x}{x - 3} + \frac{9 - 6 x}{x (x - 3)}$

$= \frac{x^{2} + 9 - 6 x}{x (x - 3)}$

$= \frac{{(x - 3)}^{2}}{x (x - 3)}$

$= \frac{x - 3}{x} .$

Câu 4:

Phân tích đa thức thành nhân tử:

$6 x^{3} y - 12 x^{2} y^{2}$

Xem đáp án

Phương pháp:

Phân tích đa thức thành nhân tử nhờ các phương pháp: nhóm hạng tử chung, đặt nhân tử chung, phương pháp hằng đẳng thức, phương pháp phối hợp các phương pháp.

Cách giải:

$6 x^{3} y - 12 x^{2} y^{2} = 6 x^{2} y (x - 2 y)$

Câu 5:

Phân tích đa thức thành nhân tử:

$x^{2} - 14 x + 49 - 4 y^{2}$

Xem đáp án

Phương pháp:

Phân tích đa thức thành nhân tử nhờ các phương pháp: nhóm hạng tử chung, đặt nhân tử chung, phương pháp hằng đẳng thức, phương pháp phối hợp các phương pháp.

Cách giải:

$x^{2} - 14 x + 49 - 4 y^{2} = {(x - 7)}^{2} - 4 y^{2} = (x - 7 + 2 y) (x - 7 - 2 y)$

Câu 6:

Phân tích đa thức thành nhân tử:

$2 x^{2} - 7 x + 5$

Xem đáp án

Phương pháp:

Phân tích đa thức thành nhân tử nhờ các phương pháp: nhóm hạng tử chung, đặt nhân tử chung, phương pháp hằng đẳng thức, phương pháp phối hợp các phương pháp.

Cách giải:

$2 x^{2} - 7 x + 5 = 2 x^{2} - 2 x - 5 x + 5 = 2 x (x - 1) - 5 (x - 1) = (2 x - 5) (x - 1)$

Câu 7:

Tìm x, biết: ${(x + 3)}^{2} - (x + 1) (x - 1) = 1$

Xem đáp án

Phương pháp:

Giải phương trình bằng phương pháp đưa về phương trình tích hoặc phương trình bậc nhất một ẩn nhờ các quy tắc nhân đa thức với đa thức và chuyển vế đổi dấu…

Cách giải:

${(x + 3)}^{2} - (x + 1) (x - 1) = 1$

$\Leftrightarrow x^{2} + 6 x + 9 - x^{2} + 1 = 1$

$\Leftrightarrow 6 x + 9 = 0$

$\Leftrightarrow 6 x = - 9$

$\Leftrightarrow x = - \frac{3}{2}$

Vậy $x = - \frac{3}{2} .$

Câu 8:

Tìm x, biết:

$(x + 1) (3 - x) + (8 - 12 x + 6 x^{2} - x^{3}) : (2 - x) = 10$

Xem đáp án

Phương pháp:

Giải phương trình bằng phương pháp đưa về phương trình tích hoặc phương trình bậc nhất một ẩn nhờ các quy tắc nhân đa thức với đa thức và chuyển vế đổi dấu…

Cách giải:

$(x + 1) (3 - x) + (8 - 12 x + 6 x^{2} - x^{3}) : (2 - x) = 10$

$\Leftrightarrow 3 x - x^{2} + 3 - x + {(2 - x)}^{3} : (2 - x) = 10$

$\Leftrightarrow - x^{2} + 2 x + 3 + {(2 - x)}^{2} = 10$

$\Leftrightarrow - x^{2} + 2 x + 3 + x^{2} - 4 x + 4 = 10$

$\Leftrightarrow - 2 x + 7 = 10$

$\Leftrightarrow 2 x = - 3$

$\Leftrightarrow x = - \frac{3}{2}$

Vậy

x = - \frac{3}{2}

Câu 9:

Cho đa thức $M (x) = x^{3} + 3 x^{2} + 3 x - 2$ và đa thức $N (x) = x + 1$

Tìm đa thức thương và đa thức dư của phép chia đa thức cho đa thức

Xem đáp án

Phương pháp:

Dựa vào quy tắc chia đa thức cho đa thức.

Cách giải:

Cho đa thức $M (x) = x^{3} + 3 x^{2} + 3 x - 2$ và đa thức $N (x) = x + 1$

Tìm đa thức thương và đa thức dư của phép chia đa thức $M (x)$ cho đa thức $N (x) .$

Ta có:

$\frac{\begin{array}{l} x^{3} + 3 x^{2} + 3 x - 2 \\ - \\ x^{3} + x^{2} \end{array}}{\begin{array}{l} 2 x^{2} + 3 x \\ - \\ \frac{2 x^{2} + 2 x}{\begin{array}{l} x - 2 \\ - \\ \frac{x + 1}{- 3} \end{array}} \end{array}}$	$x + 1$
	$x^{2} + 2 x + 1$

Vậy $M (x) : N (x)$ được thương bằng $x^{2} + 2 x + 1$ và dư 3.

Câu 10:

Cho đa thức $M (x) = x^{3} + 3 x^{2} + 3 x - 2$ và đa thức $N (x) = x + 1$

Tìm các giá trị nguyên của $x$ sao cho giá trị của đa thức $M (x)$ chia hết cho giá trị của đa thức $N (x) .$

Xem đáp án

Phương pháp:

Dựa vào quy tắc chia đa thức cho đa thức.

Cách giải:

Tìm các giá trị nguyên của $x$ sao cho giá trị của đa thức $M (x)$ chia hết cho giá trị của đa thức $N (x) .$

Điều kiện: $x \neq - 1.$

Ta có: $M (x) = N (x) . (x^{2} + 2 x + 1) - 3$

$\Leftrightarrow \frac{M (x)}{N (x)} = x^{2} + 2 x + 1 - \frac{3}{N (x)}$

$\Leftrightarrow \frac{x^{3} + 3 x^{2} + 3 x - 2}{x + 1} = x^{2} + 2 x + 1 - \frac{3}{x + 1}$

Để $M (x) ⋮ N (x) \Rightarrow 3 ⋮ (x + 1) \Rightarrow x + 1 \in U (3) = \{\pm 1; \pm 3\}$

Ta có bảng:

$x + 1$	$- 1$	1	$- 3$	3
$x$	$- 2$ (tm)	0 (tm)	$- 4$ (tm)	2 (tm)

Vậy với $x \in \{- 4; - 2; 0; 2\}$ thì $M (x)$ chia hết cho $N (x) .$

Câu 11:

Cho $Δ A B C$ nhọn $(A B < A C)$ . Kẻ đường cao $A H .$ Gọi $M$ là trung điểm của $A B, N$ là điểm đối xứng của $H$ qua $M .$

Chứng minh: Tứ giác $A N B H$ là hình chữ nhật.

Xem đáp án

Phương pháp:

Sử dụng dấu hiệu nhận biết hình chữ nhật.

Cách giải:

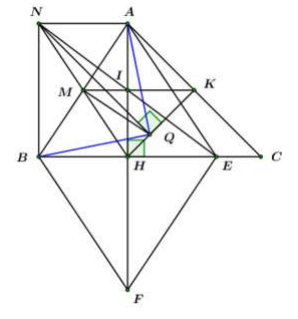
Chứng minh: Tứ giác $A N B H$ là hình chữ nhật.

Vì $N$ là điểm đối xứng của $H$ qua $M$

$\Rightarrow M$ là trung điểm của

Lại có $M$ là trung điểm của $A B (g t)$

$\Rightarrow A N B H$ là hình bình hành. (tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường).

Lại có: $∠ A H B = 90 °$ (do $A H ⊥ B C (g t)$ )

$\Rightarrow A N B H$ là hình chữ nhật. (dhnb).

Media VietJack

Câu 12:

Cho $Δ A B C$ nhọn $(A B < A C)$ . Kẻ đường cao $A H .$ Gọi $M$ là trung điểm của $A B, N$ là điểm đối xứng của $H$ qua $M .$

Trên tia đối của tia $H B$ lấy điểm $E$ sao cho $H$ là trung điểm của $B E .$ Gọi $F$ là điểm đối xứng với $A$ qua $H .$ Chứng minh: Tứ giác $A B F E$ là hình thoi.

Xem đáp án

Phương pháp

Sử dụng dấu hiệu nhận biết hình thoi.

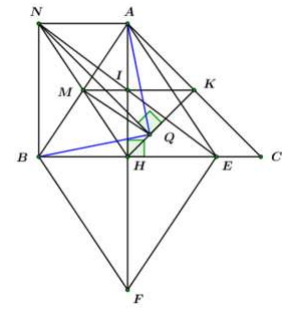
Trên tia đối của tia $H B$ lấy điểm $E$ sao cho $H$ là trung điểm của $B E .$ Gọi $F$ là điểm đối xứng với $A$ qua $H .$ Chứng minh: Tứ giác $A B F E$ là hình thoi.

Ta có: $F$ là điểm đối xứng của $A$ qua $H$

$\Rightarrow H$ là trung điểm của

Lại có: $H$ là trung điểm của BE

$\Rightarrow A B F E$ là hình bình hành. (tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường).

Lại có: $A H ⊥ B C (g t) \Rightarrow A F ⊥ B E = \{H\}$

$\Rightarrow A B F E$ là hình thoi. (dhnb)

Media VietJack

Câu 13:

Cho $Δ A B C$ nhọn $(A B < A C)$ . Kẻ đường cao $A H .$ Gọi $M$ là trung điểm của $A B, N$ là điểm đối xứng của $H$ qua $M .$

Gọi $I$ là giao điểm của $A H$ và $N E .$ Chứng minh: $M I // B C .$

Xem đáp án

Phương pháp:

Sử dụng các mối quan hệ vuông góc và song song.

Cách giải:

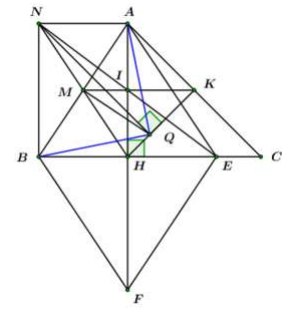
Gọi $I$ là giao điểm của $A H$ và $N E .$ Chứng minh: $M I // B C .$

Ta có: $A N B H$ là hình chữ nhật (cmt) $\Rightarrow \{\begin{cases} A N = B H \\ A N // B H \end{cases} .$ (tính chất hình chữ nhật)

Mà $B H = H E \Rightarrow B H = H E$

$\Rightarrow \{\begin{cases} A N = H E \\ A N // H E (A N // B H) \end{cases} \Rightarrow A N H E$ là hình bình hành. (dhnb)

$\Rightarrow A H \cap N E = \{I\}$ với $I$ là trung điểm của $N E$ và $A H .$

Xét $Δ A B H$ ta có:

$M, I$ lần lượt là trung điểm của và

$\Rightarrow M I$ là đường trung bình của (định nghĩa).

$\Rightarrow M I / / B H$ hay $M I / / B C$ (dpcm).

Câu 14:

Cho $Δ A B C$ nhọn $(A B < A C)$ . Kẻ đường cao $A H .$ Gọi $M$ là trung điểm của $A B, N$ là điểm đối xứng của $H$ qua $M .$

Đường thẳng $M I$ cắt $A C$ tại $K .$ Kẻ $N Q$ vuông góc với $K H$ tại $Q .$ Chứng minh: $A Q ⊥ B Q .$

Xem đáp án

Phương pháp:

Sử dụng các mối quan hệ vuông góc và song song.

Cách giải:

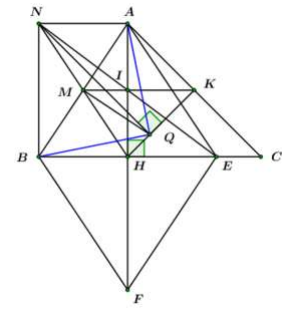
Media VietJack

Đường thẳng $M I$ cắt $A C$ tại $K .$ Kẻ $N Q$ vuông góc với $K H$ tại $Q .$ Chứng minh: $A Q ⊥ B Q .$

Ta có: $M$ là trung điểm của $N H (c m t) .$

$\Rightarrow Q M$ là đường trung tuyến ứng với cạnh huyền của $Δ N H Q$ vuông tại $Q .$

Mà $N H = A B$ (do $A N B H$ là hình chữ nhật).

Xét $Δ A Q B$ ta có:

$Q M$ là đường trung tuyến ứng với cạnh của tam giác

$Q M = \frac{1}{2} A B (c m t)$

$\Rightarrow Q M$ là đường trung tuyến ứng với cạnh huyền của

$\Rightarrow Δ A B Q$ vuông tại $Q$ hay $A Q ⊥ B Q .$ (đpcm).

CHỌN BỘ SÁCH BẠN MUỐN XEM

Bộ 14 đề thi Học kì 1 Toán 8 có đáp án

Bộ 14 đề thi Học kì 1 Toán 8 có đáp án - Đề 6

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương