Cho đường trung tuyến AM. Gọi D là trung điểm của AM, E là giao điểm của BD, AC. Chứng minh rằng
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
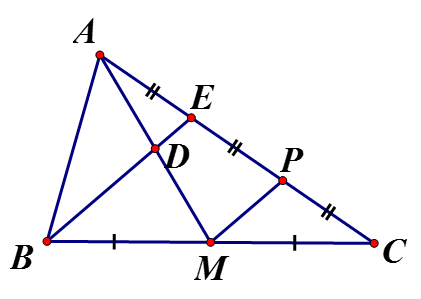
Vẽ MP//BE. Xét có: là trung điểm là trung điểm
Xét có D là trung điểm (do
=> E là trung điểm
Từ (1) và (2) suy ra