Câu hỏi:

20/07/2024 392

Cho tứ giác ABCD có BC = AD Gọi M, N, P lần lượt là trung điểm AC, CD, DB. Chứng minh $ΔMNP$ cân

Xem lời giải

Bắt Đầu Thi Thử

Trả lời:

Giải bởi qa.haylamdo.com

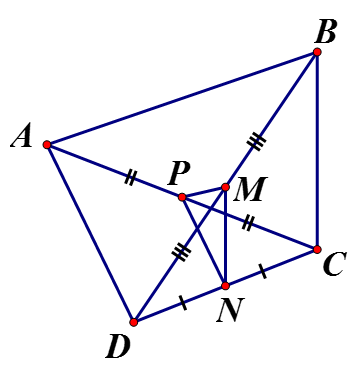
$Δ A C D$ có M là trung điểm AC, N là trung điểm CD => MN là đường trung bình $Δ A C D$

$\Rightarrow M N = \frac{1}{2} B C (1)$

Chứng minh tương tự $\Rightarrow P N$ là đường trung bình $Δ D C B \Rightarrow P N = \frac{1}{2} A D$

Mà $A D = B C$ (3)

Từ (1), (2), (3) $\Rightarrow M N = P N \Rightarrow Δ M N P$ cân tại N

Câu trả lời này có hữu ích không?

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Cho $a^{3} + b^{3} + c^{3} = 3 a b c$ . Tính $B = (1 + \frac{a}{b}) (1 + \frac{b}{c}) (1 + \frac{c}{a})$

Xem đáp án » 19/10/2022 258

Câu 2:

Cho hình thang ABCD (AB//CD), M là trung điểm AD, N là trung điểm BC. Gọi I, K lần lượt là giao điểm của MN với BD, AC. Cho biết AB = 6cm, CD = 14cm. Tính độ dài các đoạn thẳng MI, IN, KN.

Xem đáp án » 19/10/2022 193

Câu 3:

Tìm a, b, c biết: $a^{2} - 2 a + b^{2} + 4 b + 4 c^{2} - 4 c + 6 = 0$

Xem đáp án » 19/10/2022 176

Câu 4:

Tìm x biết: ${(2 x - 7)}^{3} - 27 = 0$

Xem đáp án » 19/10/2022 167

Câu 5:

Chứng minh rằng: $(a + b) (a^{2} - ab + b^{2}) + (a - b) (a^{2} + ab + b^{2}) = 2 a^{3}$

Xem đáp án » 19/10/2022 153

Câu 6:

Khai triển hằng đẳng thức: ${(x - y)}^{3}$

Xem đáp án » 19/10/2022 149

Câu 7:

Khai triển hằng đẳng thức: $8 x^{3} - y^{3}$

Xem đáp án » 19/10/2022 145

Câu 8:

Khai triển hằng đẳng thức: $64 + x^{3}$

Xem đáp án » 19/10/2022 140

Câu 9:

Cho BH là đường cao của $Δ A B C .$ Từ trung điểm M của AB, kẻ $M E ⊥ A C,$ và từ trung điểm N của cạnh BC kẻ $N P / / B H (P \in H C)$ . Chứng minh rằng:

$\begin{array}{l} a) M E / / B H \\ b) M E / / N P & M E = N P \end{array}$

Xem đáp án » 19/10/2022 130

Câu 10:

Chứng minh rằng: ${(a + b)}^{3} - 3 ab (a + b) = a^{3} + b^{3}$

Xem đáp án » 19/10/2022 115

Câu 11:

Cho $x + y + z = 0.$ Chứng minh rằng $x^{3} + y^{3} + z^{3} = 3 x y z$

Xem đáp án » 19/10/2022 113

Câu 12:

Chứng minh rằng: $(a + b) [{(a - b)}^{2} + ab] = a^{3} + b^{3}$

Xem đáp án » 19/10/2022 105

Câu 13:

Rút gọn hằng đẳng thức: $(y + 3) (y^{2} - 3 y + 9)$

Xem đáp án » 19/10/2022 102

Xem thêm các câu hỏi khác »

Đề thi liên quan

Xem thêm »

Trắc nghiệm Toán 8 Nhân đơn thức với đa thức, đa thức với đa thức có lời giải chi tiết

2 đề 9128 lượt thi Thi thử
Bài tập Nhân đơn thức với đa thức (có lời giải chi tiết)

2 đề 6105 lượt thi Thi thử
Tổng hợp bài tập Toán 8 Chương 3: Phương trình bậc nhất một ẩn

13 đề 5417 lượt thi Thi thử
Top 12 Đề kiểm tra Toán 8 Học Kì 2 Chương 3 Đại Số có đáp án, cực hay

16 đề 5247 lượt thi Thi thử
Đề thi Toán lớp 8 Giữa học kì 2 năm 2020 - 2021 có đáp án

10 đề 3806 lượt thi Thi thử
Bài tập Những hằng đẳng thức đáng nhớ (có lời giải chi tiết)

2 đề 3756 lượt thi Thi thử
Top 8 Đề kiểm tra Toán 8 Học Kì 1 Chương 1 Hình học có đáp án, cực hay

9 đề 3736 lượt thi Thi thử
Top 8 Đề kiểm tra Toán 8 Học Kì 2 Chương 4 Đại Số có đáp án, cực hay

11 đề 3068 lượt thi Thi thử
Top 8 Đề kiểm tra Đại Số Toán 8 Học Kì 1 Chương 2 có đáp án, cực hay

9 đề 2973 lượt thi Thi thử
Đề kiểm tra cuối kì 2 Toán 8 có đáp án ( Mới nhất)

26 đề 2919 lượt thi Thi thử

Xem thêm »

Hỏi bài

Câu hỏi mới nhất

Xem thêm »

3) Tính số đo các góc của $Δ D M N$ .

240 19/10/2022 Xem đáp án
2) Chứng minh: $Δ A M D = Δ B N D$ .

242 19/10/2022 Xem đáp án
Cho hình thoi ABCD có AB = BD. Gọi M, N lần lượt trên các cạnh AB, BC sao cho AM + NC = AD.

1) Chứng minh: AM = BN.

271 19/10/2022 Xem đáp án
3) Tổng độ dài (DM + DN) không đổi.

183 19/10/2022 Xem đáp án
2) $Δ A B M = Δ D B N$

197 19/10/2022 Xem đáp án
Cho hình thoi ABCD có $\hat{A} = 60 °$ . Một góc xBy thay đổi sao cho tia Bx cắt cạnh AD tại M, tia By cắt cạnh CD tại N và $\hat{x B y} = 60 °$ . Chứng minh :

1) AB = BD.

258 19/10/2022 Xem đáp án
4) Tính diện tích hình thoi ABCD.

194 19/10/2022 Xem đáp án
3) Biết chu vi của hình thoi ABCD là 8cm . Tính độ dài đường chéo BD ; AC.

196 19/10/2022 Xem đáp án
2) Gọi O là giao điểm của AC và BD. Chứng minh: $O A^{2} = \frac{3}{4} A B^{2}$ .

201 19/10/2022 Xem đáp án
Cho hình thoi ABCD có AB = BD.

1) Chứng minh: Tam giác ABD đều.

185 19/10/2022 Xem đáp án

Xem thêm »

CHỌN BỘ SÁCH BẠN MUỐN XEM

Câu hỏi:

Cho tứ giác ABCD có BC = AD Gọi M, N, P lần lượt là trung điểm AC, CD, DB. Chứng minh ΔMNP<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>ΔMNP</mi></math> cân

Trả lời:

Câu trả lời này có hữu ích không?

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Câu 2:

Cho hình thang ABCD (AB//CD), M là trung điểm AD, N là trung điểm BC. Gọi I, K lần lượt là giao điểm của MN với BD, AC. Cho biết AB = 6cm, CD = 14cm. Tính độ dài các đoạn thẳng MI, IN, KN.

Câu 3:

Câu 4:

Tìm x biết: (2x−7)3−27=0<math xmlns="http://www.w3.org/1998/Math/MathML"><msup><mfenced><mrow><mn>2</mn><mi>x</mi><mo>−</mo><mn>7</mn></mrow></mfenced><mn>3</mn></msup><mo>−</mo><mn>27</mn><mo>=</mo><mn>0</mn></math>

Câu 5:

Câu 6:

Khai triển hằng đẳng thức: (x−y)3<math xmlns="http://www.w3.org/1998/Math/MathML"><msup><mfenced><mrow><mi mathvariant="normal">x</mi><mo>−</mo><mi mathvariant="normal">y</mi></mrow></mfenced><mn>3</mn></msup></math>

Câu 7:

Cho tứ giác ABCD có BC = AD Gọi M, N, P lần lượt là trung điểm AC, CD, DB. Chứng minh $ΔMNP$ cân

Tìm x biết: ${(2 x - 7)}^{3} - 27 = 0$

Khai triển hằng đẳng thức: ${(x - y)}^{3}$