Giải bởi qa.haylamdo.com
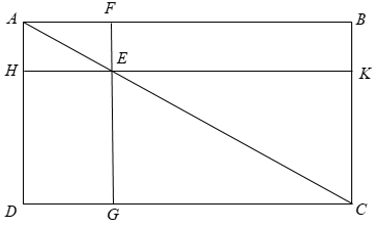
Theo giả thiết ta có FG//AD, HK//AB nên HE//AF và AH//EF.
Xét tứ giác AFEH có:
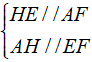
⇒ AFEH là hình bình hành.
Mà Aˆ = 900 ⇒ AFEH là hình chữ nhật.
⇒ Δ AFE = Δ AHE ( c - g - c ) → SAFE = SAHE.
Tương tự: SEKC = SEGC; SABC = SADC
⇒ SABC - SAFE - SEKC = SADC - SAHE - SEGC hay SEFBK = SEHDG.
Cho tam giác nhọn ABC, các đường cao AA', BB', CC' cắt nhau tại H. Chứng minh rằng: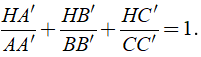 
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai ?
A. Hình vuông là đa giác đều.
B. Tổng các góc của đa giác lồi 8 cạnh là 10800.
C. Hình thoi là đa giác đều.
D. Số đo góc của hình bát giác đều là 135,50.
Chứng minh rằng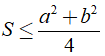 
với S là diện tích của tam giác có độ dài hai cạnh là a,b ?
Trung tuyến AD và BE của Δ ABC cắt nhau tại G. Chứng minh rằng:
SDEG = SCEG = SCED = SABG = SABE = SABC.
