Giải bởi qa.haylamdo.com
Ta có: ( 2x + 1 )( x2 + 2 ) = 0
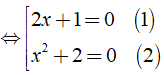
Giải ( 1 ) ⇔ 2x + 1 = 0 ⇔ 2x = - 1 ⇔ x = - 1/2.
Ta có: x2 ≥ 0 ⇒ x2 + 2 ≥ 2 ∀ x ∈ R
⇒ Phương trình ( 2 ) vô nghiệm.
Vậy phương trình đã cho có tập nghiệm S = {}.
