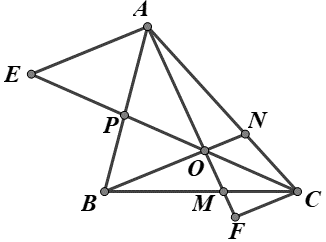
Cho tam giác ABC. Trên các cạnh BC, CA, AB lấy lần lượt các điểm M, N, P sao cho AM, BN, CP đồng qui tại O. Qua A và C vẽ các đường thẳng song song với BO cắt CO, OA lần lượt ở E và F.
Chứng minh: và
Giải bởi qa.haylamdo.com
Cho tam giác ABC có , AB = 4 cm, AC = 8 cm, Tính độ dài cạnh BC ?
Cho có 3 góc nhọn, các đường cao cắt nhau ở H. Chứng minh: tam giác AEF đồng dạng với ABC, tam giác BDF đồng dạng với EDC
AD.HD= DB.DC và suy ra các hệ thức tương tự
Tam giác ACE cân tại C.
Chứng minh:
Cho hình thang ABCD có AB//CD, AB=4cm , DB = 6cm và . Tính độ dài CD.
Cho tam giác ABC vuông tại A có AK là đường cao AB = 12cm, AC = 16cm.
Chứng minh: CAK đồng dạng với CBA
Cho tam giác ABC vuông tại A có AK là đường cao AB = 12cm, AC = 16cm.
Chứng minh: ABK đồng dạng với CAK
Cho hình thang ABCD (AB // CD). Gọi O là giao điểm của hai đường chéo AC và BD.
Chứng minh OA.OD = OB.OC.
Cho tam giác ABC có đường phân giác trong AD. Qua C kẻ đường thẳng song song với AB, cắt tia AD tại E. Chứng minh:
tam giác ABH đồng dạng với EDH và suy ra các kết quả tương tự
Cho tam giác ABC vuông tại A có AK là đường cao AB = 12cm, AC = 16cm.
Chứng minh: tam giác ABK đồng dạng với CBA. Tính độ dài đoạn thẳng BC, AK.
Cho có 3 góc nhọn, các đường cao cắt nhau ở H. Chứng minh: và suy ra các kết quả tương tự.
Điểm H cách đều 3 cạnh của tam giác DEF
