Cho hình bình hành ABCD có E, F lần lượt là trung điểm AB, CD
a) CMR: AF // EC
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
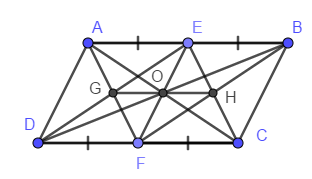
E, F Là trung điểm của AB, CD
=> AE = CF = BF = DF
Xét tứ giác AECFcó:
=> AECF Là hình bình hành (dhnb)
=> AF // CE.