Dạng 3. Chứng minh ba điểm thẳng hàng, các đường thẳng đồng quy có đáp án
-
691 lượt thi
-
8 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Cho hình bình hành ABCD có E, F lần lượt là trung điểm AB, CD
a) CMR: AF // EC
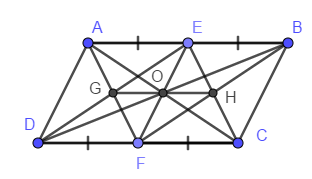
E, F Là trung điểm của AB, CD
=> AE = CF = BF = DF
Xét tứ giác AECFcó:
=> AECF Là hình bình hành (dhnb)
=> AF // CE.Câu 3:
O Là trung điểm của AC và BD (t/c hbh)
Ta có: EO là đường trung bình của
OF Là đường trung bình của
=> E; O; F thẳng hàng ( tiền đề o’clit)
Câu 4:
OH là đường trung bình của
Từ (1) và (2) (tiền đề o’clit)
=> O, H, G thẳng hàng.
Câu 5:
e) AB = CD = 4cm
Chứng minh được GH là đường trung bình của
Câu 6:
Cho hình bình hành ABCD. Lấy sao cho AN = CM .
a) CMR: AM // CN
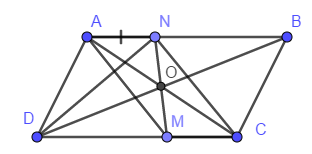
=> ANCM Là hình bình hành
Câu 7:
Mà AB = DC, AN = CM
=> BN = DM
Mà BN // DM (do AB // CD)
=> BNDM là hình bình hành
=> DN = DM.
Câu 8:
Ta có ANCM là hình bình hành; O là trung điểm của đường chéo AC
=> O Là trung điểm của MN
Từ (1) và (2) => AC, BD, MN đồng quy.
