Cho tam giác ABC có . Tính độ dài đường phân giác AD.
Giải bởi qa.haylamdo.com
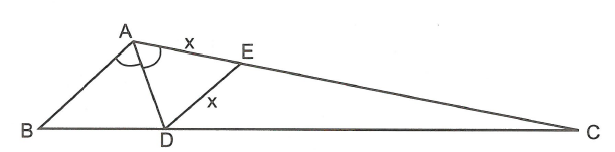
Kẻ (E thuộc AC)
Ta có: (hai góc so le trong)
đều
Đặt
Vì nên (hệ quả định lý Ta-lét)
Vậy .
Cho hình vuông ABCD. Trên cạnh AB lấy điểm I. Gọi E là giao điểm của DI và CB. Gọi J là giao điểm của AE và CI. Chứng minh BJ vuông góc với DE.
Cho hình thang ABCD , AD cắt BC tại I, AC cắt BD tại O. M, N lần lượt là trung điểm của AB, DC. Chứng minh rằng I, M, O, N thẳng hàng.
Cho tứ giác lồi ABCD. Gọi O là giao điểm của AC và BD. Gọi I, K, H lần lượt là chân đường cao kẻ từ B, O, C tới AD. Chứng minh rằng .
Cho tam giác ABC, O là một điểm thuộc miền trong tam giác. Qua O kẻ HF song song với BC, DE song song với AB, MK song song với AC (H, K thuộc AB; E, M thuộc BC; D, F thuộc AC). Chứng minh rằng:
Cho tam giác ABC với đường phân giác AD thỏa mãn . Tính số đo góc BAC.
Cho tam giác ABC nhọn AH là đường cao. Trên AH, AB, AC lần lượt lấy điểm D, E, F sao cho . Chứng minh rằng EF//BC.
