Cho hình thoi ABCD có , kẻ , rồi kéo dài một đoạn HE = BH. Nối E với A, E với D. Chứng minh :
1) H là trung điểm AD.
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
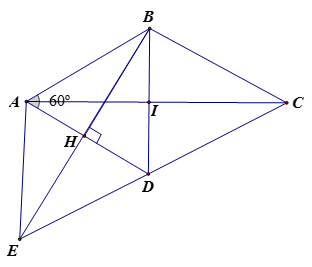
1) Ta có: AB = AD ( vì ABCD là hình thoi)
Và
Suy ra: ABD là tam giác đều.
Mà nên H là trung điểm của AD.
Cho hình thoi ABCD có AB = BD. Gọi M, N lần lượt trên các cạnh AB, BC sao cho AM + NC = AD.
1) Chứng minh: AM = BN.
Cho hình thoi ABCD có . Một góc xBy thay đổi sao cho tia Bx cắt cạnh AD tại M, tia By cắt cạnh CD tại N và . Chứng minh :
1) AB = BD.
Cho tam giác ABC cân tại A, hai đường cao BE và CF cắt nhau tại H. Đường thẳng AH cắt EF tại D , cắt BC tại G . Gọi M và N lần lượt là hình chiếu của G trên AB và AC . Chứng minh rằng tứ giác DNGM là hình thoi.
c) Hình bình hành ABCD có thêm điều kiện gì để tứ giác BCNE là hình thang cân.
Cho hình bình hành ABCD. Vẽ tại E, tại F. Biết AE = DF . Chứng minh rằng tứ giác ABCD là hình thoi.
Cho hình bình hành ABCD.Trên các cạnh AB và CD lần lượt lấy các điểm M và N sao cho AM = DN. Đường trung trực của BM lần lượt cắt các đường thẳng MN và BC tại E và F
a) Chứng minh E và F đối xứng với nhau qua AB
Cho hình thang cân ABCD (AB // CD, AB < CD). Gọi E, F, G, H lần lượt là trung điểm của AB, BC, CD , DA.
1) Chứng minh: EF = GH; EH = GF.