27 câu hỏi trắc nghiệm thuộc Dạng 6. Bài tập tự luyện có đáp án

Câu 1:

Cho hình bình hành ABCD. Vẽ $A E ⊥ B C$ tại E, $D F ⊥ A B$ tại F. Biết AE = DF . Chứng minh rằng tứ giác ABCD là hình thoi.

Xem đáp án

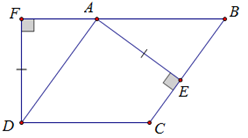
Cho hình bình hành ABCD. Vẽ AE vuông BC tại E, DF vuông AB tại F. Biết AE = DF . Chứng minh rằng tứ giác ABCD là hình thoi. (ảnh 1)

Ta có: $\hat{F A D} = \hat{A B E}$ (vì AD // BC) $\Rightarrow Δ A F D = Δ B E A$ (cgv - gn)

=> AD = AB (hai cạnh tưng ứng).

Xét hình bình hành ABCD có AD = AB nên ABCD là hình thoi.

Câu 2:

Cho tam giác ABC có AC = 2.AB, đường trung tuyến BM. Gọi H là chân đường vuông góc kẻ từ C đến tia phân giác của góc A. Chứng minh rằng ABHM là hình thoi.

Xem đáp án

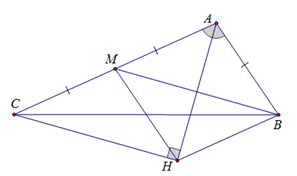
Cho tam giác ABC có AC = 2.AB, đường trung tuyến BM. Gọi H là chân đường vuông góc kẻ từ C đến tia phân giác của góc A. (ảnh 1)

+ Xét tam giác AHC vuông tại H có HM là đường trung tuyến => HM = MA = MC .

+ Ta có: $Δ M A H = Δ B A H$ (c-g-c) => HM = HB

+ Xét tứ giác ABGM có: AB = BH = HM = MA => ABHM là hình thoi.

Câu 3:

Cho hình thang cân ABCD (AB // CD, AB < CD). Gọi E, F, G, H lần lượt là trung điểm của AB, BC, CD , DA.

1) Chứng minh: EF = GH; EH = GF.

Xem đáp án

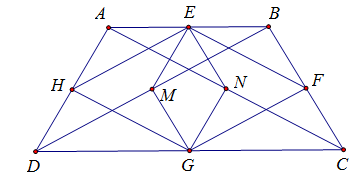
1) Vì E là trung điểm của AB, F là trung điểm của BC

=> EF là đường trung bình của tam giác ABC

=> $E F = \frac{1}{2} . A C$ (1)

Vì H là trung điểm của AD , G là trung điểm của DC

=> HG là đường trung bình của tam giác ADC

=> $H G = \frac{1}{2} . A C$ (2)

Từ (1) và (2) $\Rightarrow E F = G H = \frac{1}{2} . A C$

Chứng minh tương tự ta được EH = GF

Câu 4:

2) Chứng minh: tứ giác EFGH là hình thoi.

Xem đáp án

2) ABCD là hình thang cân => AC = BD (3)

$E F = G H = \frac{1}{2} . A C$ (4)

$E H = G F = \frac{1}{2} B D$ (5)

Từ (3), (4), (5) => EF = GH = EH = GF

Suy ra tứ giác EFGH là hình thoi

Câu 5:

3) Gọi M, N lần lượt là trung điểm BD, AC. Chứng minh: $E N = M G = \frac{B C}{2}$ .

Xem đáp án

3) Vì E là trung điểm của AB, N là trung điểm của AC

=> EN là đường trung bình của tam giác ABC

=> $E N = \frac{1}{2} B C$ (6)

Vì G là trung điểm của CD, M là trung điểm của BD

=> GM là đường trung bình của tam giác BCD

=> $M G = \frac{1}{2} B C$ (7)

Từ (6) và (7)

\Rightarrow E N = M G = \frac{1}{2} B C

(8)

Câu 6:

4) Tứ giác ENGM là hình gì? Vì sao?

Xem đáp án

4) Chứng minh tương tự ta được $M E = N G = \frac{1}{2} A D$ (9)

ABCD là hình thang cân => AD = BC (10)

Từ (8),(9),(10) => EN = MG = ME = NG

Suy ra tứ giác ENGM là hình thoi.

Câu 7:

Cho tam giác ABC cân tại A, hai đường cao BE và CF cắt nhau tại H. Đường thẳng AH cắt EF tại D , cắt BC tại G . Gọi M và N lần lượt là hình chiếu của G trên AB và AC . Chứng minh rằng tứ giác DNGM là hình thoi.

Xem đáp án

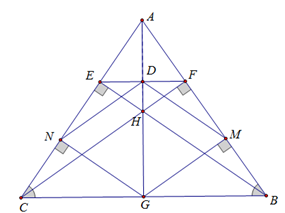
Cho tam giác ABC cân tại A, hai đường cao BE và CF cắt nhau tại H. Đường thẳng AH cắt EF tại D , cắt BC tại G . (ảnh 1)

$Δ A B E = Δ A C F$ (cạnh huyền, góc nhọn)

=> AE = AF và BE = CF .

Vì H là trực tâm của $△$ ABC nên AH là đường cao, đồng thời là đường trung tuyến, từ đó GB = GC và DE = DF.

Xét $△$ EBC có GN // BE (cùng vuông góc với AC) và GB = GC nên NE = NC.

Chứng minh tương tự ta được MF = MB .

Dùng định lí đường trung bình của tam giác ta chứng minh được DM // GN và DM = GN nên tứ giác DNGM là hình bình hành.

Mặt khác, DM = DN (cùng bằng $\frac{1}{2}$ của hai cạnh bằng nhau) nên DNGM là hình thoi.

Câu 8:

Cho hình bình hành ABCD.Trên các cạnh AB và CD lần lượt lấy các điểm M và N sao cho AM = DN. Đường trung trực của BM lần lượt cắt các đường thẳng MN và BC tại E và F

a) Chứng minh E và F đối xứng với nhau qua AB

Xem đáp án

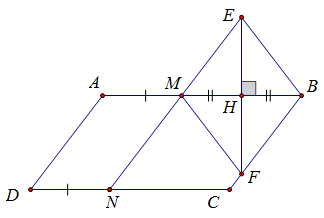
a) Gọi H là giao điểm của EF và MB.

Ta có: AMND là hình bình hành (AM = ND và AM // ND) => AD // NM.

Lại có AD // BC, nên suy ra MN // BC $\Rightarrow \hat{M E H} = \hat{H F B}$ .

Ta có: $Δ E H M = Δ F H B$ (cgv - gn) => HE = HF.

Mà $E F ⊥ A B$ nên E và F đối xứng với nhau qua AB.

Câu 9:

b) Chứng minh tứ giác MEBF là hình thoi;

Xem đáp án

b) Xét tứ giác MEBF có HE = HF, HB = HM, $E F ⊥ M B$ nên MEBF là hình thoi.

Câu 10:

c) Hình bình hành ABCD có thêm điều kiện gì để tứ giác BCNE là hình thang cân.

Xem đáp án

c) Để tứ giác BCNR là hình thang cân thì $\hat{E N C} = \hat{N E B}$ .

Ta có: $\hat{E N C} = \hat{E M B}$ (vì AB // CD); $\hat{F B H} = \hat{H B E}$ ( vì $△$ FBE cân tại B);

$\hat{M N C} = \hat{M B C}$ (vì MBCN là hình bình hành).

Xét $△$ EMB có: $\hat{E M B} = \hat{M B E} = \hat{B E M}$ nên suy ra $\hat{E M B} = \hat{M B E} = \hat{B E M} = 60 °$ .

Vậy để tứ giác BCNE là hình thang cân thì $\hat{A B C} = 60 °$ .

Câu 11:

Cho hình thoi BCNE có $\hat{A} = 60 °$ . Kẻ 2 đường cao BE và BF $(E \in A D; F \in D C)$ .

1) Chứng minh: BE = BF.

Xem đáp án

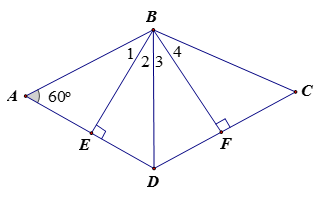
1) Vì ABCD là hình thoi nên AB = AD = CB = CD

Mặt khác $\hat{A} = 60 °$ nên $Δ A B D, Δ C B D$ đều ( vì tam giác cân có một góc bằng $60 °$ )

$\Rightarrow \hat{B_{1}} = \hat{B_{2}} = \frac{\hat{A B D}}{2} = \frac{60 °}{2} = 30 °$ và $\hat{B_{3}} = \hat{B_{4}} = \frac{\hat{D B C}}{2} = \frac{60 °}{2} = 30 °$

(trong tam giác đều thì đường cao cũng là đường phân giác).

Xét 2 tam giác vuông $△$ BED và $△$ BFD có:

$\hat{B_{2}} = \hat{B_{3}} = 30 °$

BD cạnh chung

$\Rightarrow Δ B E D = Δ B F D$ ( cạnh huyền- góc nhọn)

=> BE = BF ( hai cạnh tương ứng)

Câu 12:

2) Tính số đo

\hat{A B C}

Xem đáp án

2) Ta có:

\hat{A B C} = \hat{A B D} + \hat{D B C} = 60 ° + 60 ° = 120 °

Câu 13:

3) Tính số đo

\hat{E B F}

.

Δ B E F

là tam giác đặc biệt gì? Vì sao?

Xem đáp án

3) Ta có: $\hat{E B F} = \hat{B_{2}} + \hat{B_{3}} = 30 ° + 30 ° = 60 °$

Xét tam giác BEF có:

BE = BF

$\hat{E B F} = 60 °$

=> $△$ BEF là tam giác đều.

Câu 14:

Cho hình thoi ABCD có $\hat{A} = 60 °$ , kẻ $B H ⊥ A D (H \in A D)$ , rồi kéo dài một đoạn HE = BH. Nối E với A, E với D. Chứng minh :

1) H là trung điểm AD.

Xem đáp án

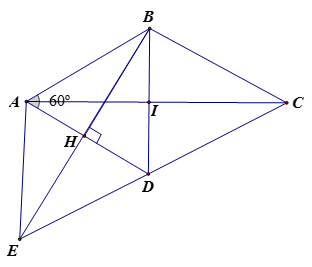
1) Ta có: AB = AD ( vì ABCD là hình thoi)

Và $\hat{A} = 60 °$

Suy ra: ABD là tam giác đều.

Mà $B H ⊥ A D$ nên H là trung điểm của AD.

Câu 15:

2) Tứ giác ABDE là hình thoi.

Xem đáp án

2) Xét tứ giác ABDE có:

HA = HD( chứng minh trên)

HE = HB (Giả thiết)

=> ABDE là hình bình hành.

Mặc khác: $A D ⊥ B E$ nên ABDE là hình thoi

( vì hình bình hành có hai đường chéo vuông góc với nhau là hình thoi).

Câu 16:

3) D là trung điểm CE .

Xem đáp án

3) Ta có:

ABCD là hình thoi => DC = AB, DC // AB (1)

ABDE là hình thoi => DE = AB, DE // AB (2)

Từ (1), (2) suy ra C, D, E thẳng hàng ( theo tiên đề Ơclit) và DC = DE .

Vậy D là trung điểm của CE.

Câu 17:

4) AC = BE

Xem đáp án

4) Ta có:

AC = 2AI ( vì ABCD là hình thoi)

BE = 2BH ( vì ABDE là hình thoi)

Mà BH = AI ( cùng là đường cao của tam giác đều ABD)

=> AC = BE.

Câu 18:

Cho hình thoi ABCD có AB = BD.

1) Chứng minh: Tam giác ABD đều.

Xem đáp án

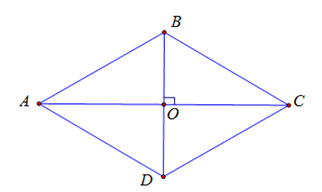
1) ABCD là hình thoi => AB = AD mà AB = BD (giả thiết)

Nên AB = AD = BD.

Vậy $△$ ABD là tam giác đều.

Câu 19:

2) Gọi O là giao điểm của AC và BD. Chứng minh: $O A^{2} = \frac{3}{4} A B^{2}$ .

Xem đáp án

2) Tam giác OAB vuông tại O $\Rightarrow O A^{2} = A B^{2} - O B^{2}$ mà $O B = \frac{B D}{2} = \frac{A B}{2} \Rightarrow O B^{2} = \frac{A B^{2}}{4}$ .

Do đó :

O A^{2} = A B^{2} - \frac{A B^{2}}{4} = \frac{3}{4} A B^{2}

Câu 20:

3) Biết chu vi của hình thoi ABCD là 8cm . Tính độ dài đường chéo BD ; AC.

Xem đáp án

3) Chu vi ABCD là 8 cm $\Rightarrow B D = A B = 2 cm$ nên $B O = \frac{B D}{2} = 1 cm$ .

Tam giác vuông OAB : $A O^{2} = A B^{2} - O B^{2} = 4 - 1 = 3 \Rightarrow A O = \sqrt{3} cm$ .

$A C = 2 A O = 2 \sqrt{3} cm$ . Vậy $B D = 2 cm, A C = 2 \sqrt{3} cm$ .

Câu 21:

4) Tính diện tích hình thoi ABCD.

Xem đáp án

4) Diện tích hình thoi ABCD:

\frac{1}{2} A C . B D = \frac{1}{2} 2 \sqrt{3} .2 = 2 \sqrt{3} ({cm}^{2})

Câu 22:

Cho hình thoi ABCD có $\hat{A} = 60 °$ . Một góc xBy thay đổi sao cho tia Bx cắt cạnh AD tại M, tia By cắt cạnh CD tại N và $\hat{x B y} = 60 °$ . Chứng minh :

1) AB = BD.

Xem đáp án

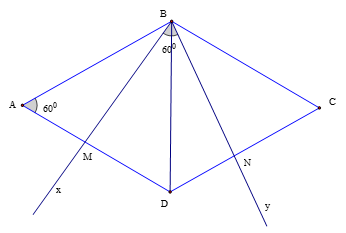
1) Chứng minh AB = BD

Ta có ABCDlà hình thoi nên:

AB = AD => $△$ ABD cân tại A

Mà $\hat{A} = 60 °$ (giả thiết) nên suy ra $△$ ABD đều.

=> AB = BD .

Câu 23:

2)

Δ A B M = Δ D B N

Xem đáp án

2) Chứng minh $Δ A B M = Δ D B N$

Xét $Δ A B M$ và $Δ D B N$ có:

$\hat{B A M} = \hat{B D N} = 60^{°}$ (Gt)

AB = AD (cmt)

$\hat{A B M} = \hat{D B N}$ (Cùng cộng với $\hat{M B D}$ tạo thành góc có số đo $60 °$ )

=> $Δ A B M = Δ D B N$ (g.c.g).

Câu 24:

3) Tổng độ dài (DM + DN) không đổi.

Xem đáp án

3) Chứng minh tổng độ dài (DM + DN) không đổi.

Do $Δ A B M = Δ D B N$ (cmt) nên AM = DN (1)

Từ (1) suy ra: $D M + D N = D M + A M \Rightarrow D M + D N = A D$ .

Vì AD không đổi nên (DM + DN) không đổi.

Câu 25:

Cho hình thoi ABCD có AB = BD. Gọi M, N lần lượt trên các cạnh AB, BC sao cho AM + NC = AD.

1) Chứng minh: AM = BN.

Xem đáp án

1) Theo bài ra ta có: $A M + N C = A D$

Lại có: BN + NC = BC = AD (ABCD là hình thoi)

=> AM = BN.

Câu 26:

2) Chứng minh: $Δ A M D = Δ B N D$ .

Xem đáp án

2) +Có: AB = AD (ABCD là hình thoi)

+ Lại có: AB = BD (GT)

=> AD = BD = AB

$\Rightarrow$ $Δ A B D$ là tam giác đều.

$\Rightarrow \hat{B A D} = 60 ° \Rightarrow \hat{M A D} = 60 ° (1)$

+ Có: $\hat{A B D} = \hat{C B D} = \frac{\hat{A B C}}{2}$ (abcd là hình thoi)

+Lại có: $\hat{A B D} = 60 °$ ( $Δ A B D$ là tam giác đều)

$\Rightarrow \hat{C B D} = 60 ° \Rightarrow \hat{N B D} = 60 ° (2)$

+Từ (1) và (2) ta có: $\hat{M A D} = \hat{N B D}$

+ Xét $Δ A M D$ và $Δ B N D$ có:

$A M = B N (C M T) \hat{M A D} = \hat{N B D} (C M T) A D = B D (C M T)$

$\Rightarrow Δ A M D = Δ B N D$ (c.g.c)

Câu 27:

3) Tính số đo các góc của $Δ D M N$ .

Xem đáp án

3) + Có $Δ A M D = Δ B N D$ (CMT)

=> $\hat{M D A} = \hat{N D B}$ (cặp góc tương ứng)

+ Mà: $\hat{M D A} + \hat{M D B} = \hat{A D B} = 60 °$

=> $\hat{N D B} + \hat{M D B} = 60 ° \Rightarrow \hat{M D N} = 60 °$

+ Có $Δ A M D = Δ B N D$ (CMT)

=> MD = ND (cặp cạnh tương ứng)

=> $Δ M N B$ là tam giác cân tại D, mà $\hat{M D N} = 60 °$

=> $Δ M N B$ là tam giác đều

=> $\hat{N M D} \hat{= M N D} = \hat{M D N} = 60 °$ .

CHỌN BỘ SÁCH BẠN MUỐN XEM

Bài tập Toán 8 Chủ đề 14: Hình thoi có đáp án

Dạng 6. Bài tập tự luyện có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương