Cho ∆ABC nhọn (AB > AC) nội tiếp đường tròn (O), kẻ đường cao AH của ∆ ABC và đường kính AD của (O). Gọi M là hình chiếu vuông góc của B trên đường thẳng AD.
1) Chứng minh tứ giác ABMH nội tiếp.
2) Tiếp tuyến tại D của đường tròn (O) cắt hai tia AB và AC lần lượt tại E và F. Chứng minh AB.AE = AC.AF.
3) Gọi I là trung điểm của BC, đường thẳng qua I song song với CD cắt BM tại K, tia DK cắt đường tròn (O) tại điểm thứ hai là S. Hai đường thẳng BC và EF cắt nhau tại Q. Chứng minh tứ giác SBKI nội tiếp và SQ là tiếp tuyến của (O).
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
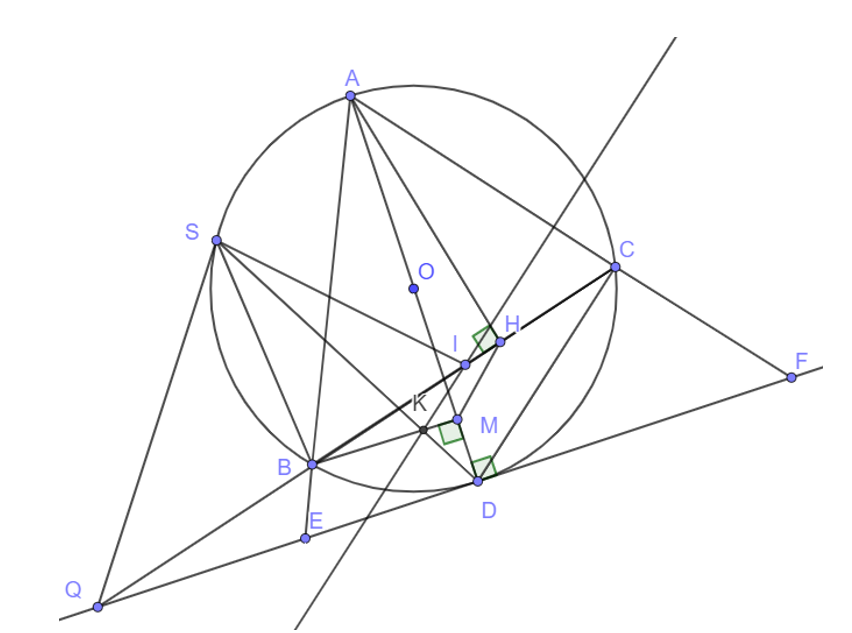
1) Vì AH là đường cao của ∆ ABC nên = 90°.
Vì M là hình chiếu vuông góc của B trên đường thẳng AD nên = 90°.
Suy ra = 90°.
Do đó H và M là hai đỉnh liên tiếp cùng nhìn AB dưới một góc bằng nhau và bằng 90°.
Vì vậy tứ giác ABHM nội tiếp.
2) Nối B với D và D với C.
Xét đường tròn (O) ta có:
= 90° (góc nội tiếp chắn đường kính AD).
![]() BD ⊥ AE, DC ⊥ AF
BD ⊥ AE, DC ⊥ AF
Xét ∆ADE vuông tại D, có DB là đường cao:
Áp dụng hệ thức lượng ta có: AB. AE = AD2
Xét ∆ADF vuông tại D, có DC là đường cao:
Áp dụng hệ thức lượng ta có:AC.AF = AD2
Do đó: AB. AE = AC.AF (đpcm).
3) Vì IK // CD nên = (2 góc định vị) (1)
Xét đường tròn (O) ta có: (góc nội tiếp chắn cung BD) (2)
Từ (1) và (2) suy ra tứ giác SBKI nội tiếp ![]() (1)
(1)
Vì I là trung điểm BC ![]() OI ⊥ BC
OI ⊥ BC ![]() => = 90°
=> = 90°
![]() = 90° và cùng chắn cung OB nên: Tứ giác OIMB nội tiếp
= 90° và cùng chắn cung OB nên: Tứ giác OIMB nội tiếp
![]() (2)
(2)
Từ (1) và (2) suy ra:
![]() Tứ giác OISD nội tiếp => O, I, S, D thuộc một đường tròn (3)
Tứ giác OISD nội tiếp => O, I, S, D thuộc một đường tròn (3)
Vì = 90° và cùng chắn cung OQ nên: Tứ giác OIDQ nội tiếp ![]() O, I, D, Q thuộc một đường tròn (4)
O, I, D, Q thuộc một đường tròn (4)
Từ (3) và (4) suy ra: O, I, D, Q, S thuộc một đường tròn
=> Tứ giác OSQD nội tiếp
=> = 90°
=> = 180°
=> = 180° − 90° = 90°
=> OS ⊥ SQ
=>SQ là tiếp tuyến (O) (đpcm)
1)Giải bài toán bằng cách lập phương trình hoặc hệ phương trình.
Một hội trường có 100 ghế ngồi được kê thành những dãy ghế, mỗi dãy ghế có số ghế ngồi như nhau. Sau đó, khi sửa chữa người ta đã bổ sung thêm 5 dãy ghế. Để đảm bảo số chỗ ngồi của hội trường như ban đầu, mỗi dãy ghế được kê ít hơn so với ban đầu là 1 ghế. Hỏi ban đầu, hội trường có bao nhiêu dãy ghế?
2) Chiếc mũ sinh nhật là một hình nón được làm từ bìa cứng có đường kính đáy là 36cm, độ dài đường sinh là 35cm. Hãy tính diện tích phần bìa cứng để làm chiếc mũ nói trên. (Bỏ qua mép gấp và cho π ≈ 3,14).
Trong mặt phẳng Oxy, cho parabol (P): y = x2 và đường thẳng (d): y = 4x − m + 1.
1)Tìm tọa độ giao điểm của (d) và (P) khi m = 4.
2) Gọi hoành độ giao điểm của (P) và (d) là x1, x2. Tìm m để = .
Với các số thực x, y thỏa mãn x − = − y. Tìm giá trị lớn nhất của biếu thức P = x + y