12 câu hỏi trắc nghiệm thuộc Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)- Đề 1

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)

Đề số 1
Đề số 2
Đề số 3
Đề số 4
Đề số 5
Đề số 6
Đề số 7
Đề số 8
Đề số 9
Đề số 10
Đề số 11
Đề số 12
Đề số 13
Đề số 14
Đề số 15
Đề số 16
Đề số 17
Đề số 18
Đề số 19
Đề số 20
Đề số 21
Đề số 22
Đề số 23
Đề số 24
Đề số 25
Đề số 26
Đề số 27
Đề số 28
Đề số 29
Đề số 30

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)- Đề 1

4914 lượt thi
12 câu hỏi
45 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Giải các phương trình và hệ phương trình sau đây :

$a) \frac{x}{\sqrt{3}} + \sqrt{3} x = \sqrt{3}$

Xem đáp án

$\begin{array}{l} a) \frac{x}{\sqrt{3}} + \sqrt{3} x = \sqrt{3} \Leftrightarrow \frac{x + 3 x}{\sqrt{3}} = \sqrt{3} \\ \Leftrightarrow x + 3 x = 3 \Leftrightarrow 4 x = 3 \Leftrightarrow x = \frac{3}{4} \\ S = \{\frac{3}{4}\} \end{array}$

Câu 2:

Giải các phương trình và hệ phương trình sau đây :

$b) x^{2} + 6 x - 5 = 0$

Xem đáp án

b) Phương trình $x^{2} + 6 x - 5 = 0$ có $Δ' = 3^{2} - 1. (- 5) = 14 > 0$ nên phương trình có hai nghiệm phân biệt:

$x_{1} = - 3 + \sqrt{14}; x_{2} = - 3 - \sqrt{14}$

Câu 3:

Giải các phương trình và hệ phương trình sau đây :

$c) \{\begin{cases} \sqrt{2} x + y = \sqrt{2} + 2 \\ 2 \sqrt{2} x - y = 2 \sqrt{2} - 2 \end{cases}$

Xem đáp án

c, $\{\begin{cases} \sqrt{2} x + y = \sqrt{2} + 2 \\ 2 \sqrt{2} x - y = 2 \sqrt{2} - 2 \end{cases} \Leftrightarrow \{\begin{cases} y = \sqrt{2} + 2 - \sqrt{2} x \\ 3 \sqrt{2} x = 3 \sqrt{2} \end{cases} \Leftrightarrow \{\begin{cases} x = 1 \\ y = 2 \end{cases}$

Hệ phương trình có nghiệm duy nhất

(x; y) = (1; 2)

Câu 4:

Cho hàm số có đồ thị là Parabol (P): a, Vẽ đồ thị (P) của hàm số đã cho

Xem đáp án

a) Học sinh tự vẽ Parabol

Câu 5:

b, Qua điểm $A (0; 1)$ vẽ đường thẳng song song với trục hoành Ox cắt (P) tại hai điểm Evà F Viết tọa độ của E và F.

Xem đáp án

b, Đường thẳng đi qua A(0;1) và song song với trục hoành có phương trình y=1

Xét phương trình hoành độ giao điểm của đường thẳng y=1 và parabol $y = 0,25 x^{2}$ , ta có: $0,25 x^{2} = 1 \Leftrightarrow x^{2} = 4 \Leftrightarrow [\begin{array}{l} x = 2 \Rightarrow y = 1 \\ x = - 2 \Rightarrow y = 1 \end{array}$

Vậy hai điểm E và F có tọa độ lần lượt là $(- 2; 1)$ và $(2; 1)$

Câu 6:

Cho phương trình bậc hai $x^{2} - (m + 2) x + 2 m = 0 (*)$ (m là tham số)

a) Chứng minh rằng phương trình $(*)$ luôn có nghiệm với mọi số m

Xem đáp án

$x^{2} - (m + 2) x + 2 m = 0 (*)$

Có: $Δ = {(m + 2)}^{2} - 4.2 m = m^{2} + 4 m + 4 - 8 m = m^{2} - 4 m + 4 = {(m - 2)}^{2} \geq 0 (\forall m)$

$\Rightarrow$ Phương trình (*) luôn có hai nghiệm với mọi m

Câu 7:

b, Tìm các giá trị của m để phương trình $(*)$ luôn có hai nghiệm $x_{1}, x_{2}$ thỏa mãn

- 1 \leq \frac{2 (x_{1} + x_{2})}{x_{1} x_{2}} \leq 1

Xem đáp án

b) Gọi $x_{1}, x_{2}$ là hai nghiệm của phương trình (*)

Áp dụng hệ thức Vi-et ta có: $\{\begin{cases} x_{1} + x_{2} = m + 2 \\ x_{1} x_{2} = 2 m \end{cases}$

Theo đề bài ta có: $- 1 \leq \frac{2 (x_{1} + x_{2})}{x_{1} x_{2}} \leq 1 \Leftrightarrow - 1 \leq \frac{2 (m + 2)}{2 m} \leq 1$

\Leftrightarrow \{\begin{cases} 2 m \neq 0 \\ \frac{m + 2}{m} \geq - 1 \\ \frac{m + 2}{m} \leq 1 \end{cases} \Leftrightarrow \{\begin{cases} m \neq 0 \\ \frac{m + 2 + m}{m} \geq 0 \\ \frac{m + 2 - m}{m} \leq 0 \end{cases} \Leftrightarrow \{\begin{cases} m \neq 0 \\ \frac{2 m + 2}{m} \geq 0 \\ \frac{2}{m} \leq 0 \end{cases} \Leftrightarrow \{\begin{cases} m \neq 0 \\ [\begin{array}{l} m > 0 \\ m \leq - 1 \end{array} \\ m < 0 \end{cases} \Rightarrow m \leq - 1

Vậy $m \leq 1$ thỏa mãn bài toán

Câu 8:

Cho tam giác ABC vuông tại A có $A B = 4 c m, A C = 3 c m .$ Lấy điểm D thuộc cạnh AB $(A D < D B) .$ Đường tròn (O) đường kính BD cắt CB tại E. Kéo dài CD cắt đường tròn (O) tại F

a,Chứng minh rằng $A C E D$ là tứ giác nội tiếp

Xem đáp án

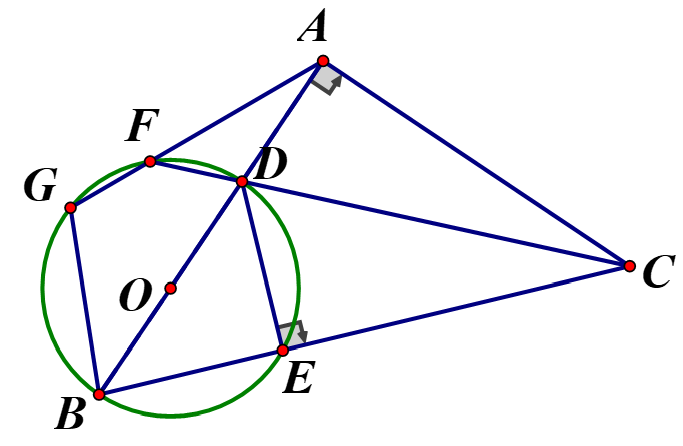
Cho tam giác AB C vuông tại A có AB = 4cm, AC = 3cm Lấy điểm D thuộc cạnh AB (AD< DB) Đường tròn (O) đường kính BD cắt CB tại E. (ảnh 1)

a, Ta có

\hat{B E D} = 90^{0}

(góc nội tiếp chắn nửa đường tròn)

\Rightarrow D E ⊥ B C \Rightarrow \hat{C E D} = 90^{0}

Xét tứ giác $A C E D$ có $\hat{C A D} + \hat{C E D} = 90^{0} + 90^{0} = 180^{0}$

$\to$ Tứ giác ACED là tứ giác nội tiếp.

Câu 9:

b, Biết $B F = 3 c m .$ Tính BC và diện tích tam giác BFC

Xem đáp án

Áp dụng định lý Pytago trong tam giác vuông ABC ta có:

$B C^{2} = A B^{2} + A C^{2} = 4^{2} + 3^{2} = 16 + 9 = 25 \Rightarrow B C = \sqrt{25} = 5 (c m)$

Ta có $\hat{B F D} = 90^{0}$ (góc nội tiếp chắn nửa đường tròn)

$\Rightarrow B F ⊥ F D$ hay $B F ⊥ F C \Rightarrow Δ B F C$ vuông tại F

Áp dụng định lý Pytago trong $Δ B F C$ vuông ta có:
$F C^{2} = B C^{2} - B F^{2} = 5^{2} - 3^{2} = 16 \Rightarrow F C = \sqrt{16} = 4 (c m)$

$S_{B F C} = \frac{1}{2} F B . F C = \frac{1}{2} .3.4 = 6 (c m^{2})$

Câu 10:

c, Kéo dài AF cắt đường tròn (O) tại điểm G. Chứng minh rằng BA là tia phân giác của $\hat{C B G}$

Xem đáp án

c) Nhận thấy bốn điểm $B, D, F, G$ cùng thuộc (O) $\Rightarrow$ Tứ giác BDFG là tứ giác nội tiếp.

$\Rightarrow \hat{G B D} = \hat{A F D} = \hat{A F C} (1)$ (góc ngoài bằng góc trong tại đỉnh đối diện)

Xét tứ giác AFBC có $\hat{B A C} = \hat{B F C} = 90^{0} \Rightarrow$ Tứ giác AFBC là tứ giác nội tiếp (Tứ giác có hai đỉnh kề cùng nhìn một cạnh dưới các góc bằng nhau).

Do đó: $\hat{A B C} = \hat{A F C} (2)$ (hai góc nội tiếp cùng chắn $\overset{⏜}{A C})$

Từ (1) và (2) $\Rightarrow \hat{G B D} = \hat{A B C} \Rightarrow B A$ là tia phân giác của $\hat{C B G} (d f c m)$

Câu 11:

Trường A tiến hành khảo sát 1500 học sinh về sự yêu thích hội họa, thể thao, âm nhạc và các yêu thích khác. Mỗi học sinh chỉ chọn một yêu thích. Biết số học sinh yêu thích hội họa chiếm tỉ lệ 20% so với số học sinh toàn trường. Số học sinh yêu thích thể thao hơn số học sinh yêu thích âm nhạc là 30 học sinh, số học sinh yêu thích thể thao và hội họa bằng với số học sinh yêu thích âm nhạc và yêu thích khác.

a) Tính số học sinh yêu thích hội họa

Xem đáp án

a, Vì số học sinh yêu thích hội họa chiếm tỉ lệ 20% so với số học sinh toàn trường , nên số học sinh yêu thích hội họa là :

$1500.20 % = 300$ (học sinh)

Câu 12:

b, Hỏi tổng số học sinh yêu thích thể thao và âm nhạc là bao nhiêu ?

Xem đáp án

b) Gọi số học sinh yêu thích thể thao là x (học sinh) $(30 < x < 1200, x \in ℕ *)$

Số học sinh chọn yêu thích khác là y (học sinh) $(y < 1200, y \in ℕ *)$

Số học sinh yêu thích thể thao hơn số học sinh yêu thích âm nhạc là 30 học sinh $\to$ số học sinh yêu thích âm nhạc là x-30(học sinh)

Tổng số học sinh của trường là 1500 học sinh, số học sinh yêu thích hội họa là 300 học sinh nên số học sinh yêu thích thể thao, âm nhạc và các yêu thích khác :

$1500 - 300 = 1200$ (học sinh)

Khi đó ta có phương trình: $x + x - 30 + y = 1200 \Leftrightarrow 2 x + y = 1230 (1)$

Số học sinh yêu thích thể thao và hội họa bằng số học sinh yêu thích âm nhạc và các yêu thích khác nên ta có phương trình: $x + 300 = x - 30 + y \Leftrightarrow y = 330 (t m)$

Thay y= 330 vào phương trình (1) ta được:

$2 x = 1230 - y = 1230 - 330 = 900 \Leftrightarrow x = 450 (t m)$

Suy ra số học sinh yêu thích âm nhạc : $450 - 30 = 420$ (học sinh)

Vậy tổng số học sinh yêu thích thể thao và âm nhạc là:

$450 + 42 = 870$ (học sinh)

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)- Đề 1

Danh sách câu hỏi

Bài thi liên quan