Cho tứ giác ABCD có bốn đỉnh thuộc đường tròn . Gọi M, N, P, Q lần lượt là điểm chính giữa các cung AB, BC, CD, DA. Chứng minh rằng : .
Giải bởi qa.haylamdo.com
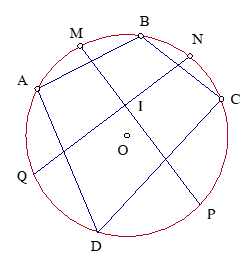
Gọi I là giao điểm của MP và NQ. Ta có.
= (sđ + sđ )
= . (sđ + sđ + sđ + sđ ).
= . Vậy MP ^ NQ.
Cho đường tròn (O), hai đường kính AB và CD vuông góc với nhau, điểm M thuộc cung nhỏ BC. Gọi E là giao điểm của MA và CD, F là giao điểm của MD và AB. Chứng minh rằng:
a)
b) Khi M di động trên cung nhỏ BC thì diện tích tứ giác AEFD không đổi.
