Cho (P): y = x2 và (d): y = 4x – 3
a) Vẽ đồ thị (P).
b) Xác định tọa độ các giao điểm của (P) và (d) bằng phép tính.
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
a) Vẽ (P)
|
x |
−2 |
−1 |
0 |
1 |
2 |
|
y = x2 |
4 |
1 |
0 |
1 |
4 |
Trên mặt phẳng tọa độ lấy các điểm: A(−2; 4); B(1; −1); O(0; 0); C(1; 1); D(2; 4).
Vẽ (d).
Đường thẳng (d): y = 4x – 3 có a = 4, b = −3 đi qua tọa độ 2 điểm M(0; b) và N
Do đó, hai điểm thuộc đường thẳng (d) là M(0; −3) và N .
Ta có đồ thị hàm số:
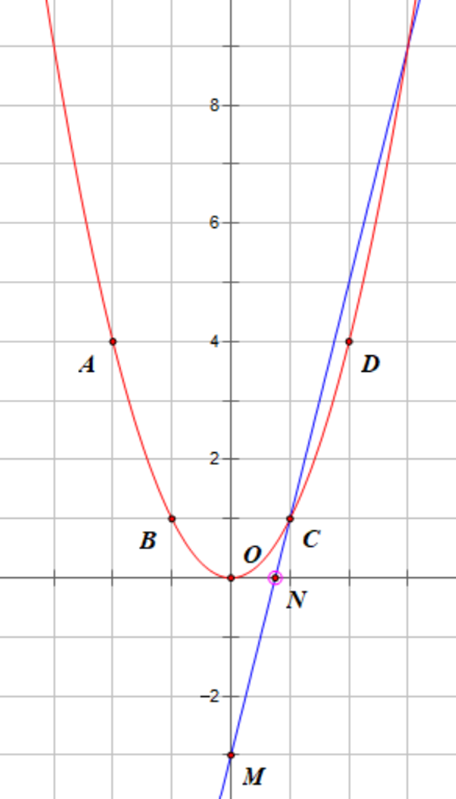
b) Phương trình hoành độ giao điểm của (P) và (d) là:
x2 = 4x – 3
Û x2 – 4x + 3 = 0
Û x2 – 3x – x + 3 = 0
Û x(x – 3) – (x – 3) = 0
Û (x – 3)(x – 1) = 0
Û Û .
∙ Với x = 3 vào (d): y = 4x – 3 = 4.3 – 3 = 9;
∙ Với x = 1 vào (d): y = 4x – 3 = 4.1 – 3 = 1.
Vậy giao điểm của (P) và (d) là (3; 9) và (1; 1).
Cho điểm A nằm ngoài đường tròn (O). Từ A kẻ hai tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). Gọi D là trung điểm của AB. Đường thẳng DC cắt đường tròn tại E (E khác C). Chứng minh:
a) Tứ giác ABOC nội tiếp.
b) DB2 = DE.DC
c)
Cho phương trình ẩn x: x2 + 2(m + 3)x + 2m – 11 = 0 (1)
a) Chứng tỏ phương trình (1) luôn có hai nghiệm phân biệt với mọi giá trị của m.
b) Tìm giá trị của m để phương trình (1) có hai nghiệm x1, x2 thỏa mãn hệ thức:
= 2.
a) Tính chiều cao của một hình trụ có bán kính đáy R = 7 cm và diện tích xung quanh bằng 112p cm2.
b) Tính độ dài cung 30° của một đường tròn có bán kính 5 dm.
Trong đợt dịch Covid-19, nhân viên y tế của một trường THCS đã mua một số hộp khẩu trang gồm 2 loại. Biết nếu mua 6 hộp loại thứ nhất và 3 hộp loại thứ hai thì hết 2 280 000 đồng; nếu mua 3 hộp loại thứ nhất và 7 hộp loại thứ hai thì hết 2 680 000 đồng. Tính giá tiền mỗi loại hộp khẩu trang.