Chứng minh đồ thị hàm số y = mx - m - 3 luôn đi qua điểm cố định với mọi giá trị của m

Biết rằng đồ thị của hàm số y = ax + 5 đi qua điểm A(-1; 3). Tìm a. Vẽ đồ thị hàm số với a vừa tìm được.

Cho hàm số y = 2x - 1 và y = -2x + 3

a) Xét tính đồng biến, nghịch biến của hai hàm số trên.

b) Vẽ hai đồ thị hàm số trên cùng một mặt phẳng tọa độ

c) Tìm tọa độ giao điểm bằng phép tính.

Cho đường tròn (O; 3cm), AB = 4 cm.

a) Tính khoảng cách từ tâm O đến dây AB.

b) M là điểm sao cho OM = 2cm. Vẽ dây $CD\perp OM$ tại M. So sánh AB và CD.

Cho $\Delta ABC$ nội tiếp đường tròn (O; R) có $\widehat{A}={80}^0,\widehat{C}={50}^0.$ Gọi O khoảng cách từ O đến AB, AC, BC lần lượt là OH, OK, OD. So sánh các độ dài OH, OK, OD.

Vẽ đồ thị y = x + 1 và y = -x +3 trên cùng một mặt phẳng tọa độ

Tìm tọa độ giao điểm C bằng phép tính. Hai đường thẳng cắt trục Ox theo thứ tự A, B. Tìm tọa độ A, B, C.

Tính chu vi và diện tích của tam giác ABC (theo đơn vị cm)

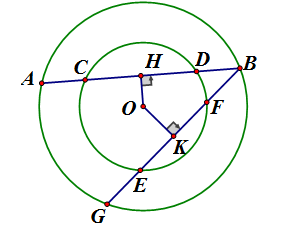
Cho 2 đường tròn đồng tâm O như hình vẽ, biết AB > BG. So sánh độ dài:

a) OH và OK                              

b) CD và EF

Cho ba đường thẳng

$y=\frac{2}{5}x+\frac{1}{2}\left(d_1\right)y=\frac{3}{5}x-\frac{5}{2}\left(d_2\right)y=kx+3,5\left(d_3\right)$

Tìm giá trị của k để ba đường thẳng trên đồng quy.