Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O) có trực tâm là điểm H. Gọi M là điểm trên dây cung BC không chứa điểm A (M khác B,C). Gọi N, P theo thứ tự là các điểm đối xứng của M qua các đường thẳng AB, AC.
a) Chứng minh AHCP là tứ giác nội tiếp.
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
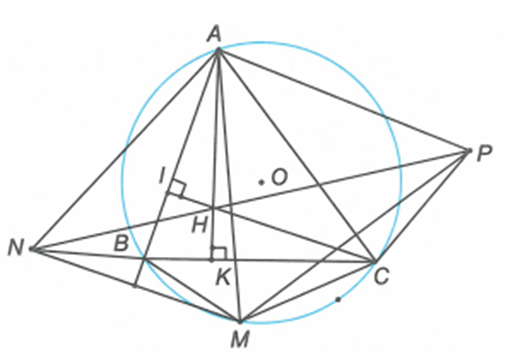
Giả sử các đường cao của tam giác là AK, CI. Để chứng minh AHCP nội tiếp ta sẽ chứng minh AHC + APC = 120°.
Ta có: AHC = IHK (đối đỉnh),
APC = AMC = ABC (do tính đối xứng và góc nội tiếp cùng chắn một cung).
Lại có tứ giác BIHK là tứ giác nội tiếp nên ABC + IHK = 180 => AHC + APC = 180.
Cho nửa đường tròn (O) đường kính AB = a. Gọi Ax, By là các tia vuông góc với AB (Ax, By thuộc cùng một nửa mặt phẳng bờ AB). Qua điểm M thuộc nửa đường tròn (O) (M khác A và B) kẻ tiếp tuyến với nửa đường tròn (O); nó cắt Ax, By lần lượt ở E và F.
a) Chứng minh: EOF = 90.
Cho đường tròn (O;R) với dây cung AB không đi qua tâm. Lấy S là một điểm bất kì trên tia đối của tia AB (S khác A). Từ điểm S vẽ hai tiếp tuyến SC, SD với đường tròn (O;R) sao cho điểm C nằm trên cung nhỏ AB (C,D là các tiếp điểm). Gọi H là trung điểm của đoạn thẳng AB.
a) Chứng minh năm điểmC, D, H, O, S thuộc đường tròn đường kính SO.
Cho điểm M thuộc cung nhỏ BC của đường tròn (O). Một đường thẳng d ở ngoài (O) và vuông góc với đường thẳng OM; đường thẳng CM,BM cắt d lần lượt tại D, E. Chứng minh rằng B , C , D , E cùng thuộc một đường tròn.
Cho đường tròn tâm (O) đường kính AB có bán kính R, tiếp tuyến Ax. Trên tiếp tuyến Ax lấy điểm F sao cho BF cắt đường tròn tại C, tia phân giác của góc ABF cắt Ax tại E và cắt đường tròn tại D.
a) Chứng minh OD // BC
Từ một điểm A nằm ngoài đường tròn ( O ; R ) ta vẽ hai tiếp tuyến AB, AC với đường tròn (B,C là tiếp điểm). Trên cung nhỏ BC lấy một điểm M, vẽ MI AB, MK AC ( I AB , K AC).
a) Chứng minh AIMK là tứ giác nội tiếp đường tròn.
Cho nửa đường tròn tâm O đường kính AB = 2R và tia tiếp tuyến Ax cùng phía với nửa đường tròn đối với AB. Từ điểm M trên Ax kẻ tiếp tuyến thứ hai MC với nửa đường tròn (C là tiếp điểm), AC cắt OM tại E; MB cắt nửa đường tròn ( O ) tại D (D khác B). Chứng minh AMCO và AMDE là các tứ giác nội tiếp đường tròn.
c) Đường thẳng EM cắt cạnh AD và BC của hình thang lần lượt ở H và K. Chứng minh M là trung điểm HK.
Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Vẽ AC, AD theo thứ tự là đường kính của hai đường tròn (O) và (O').
a) Chứng minh ba điểm C, B, D thẳng hàng.
c) Chứng minh ba đường thẳng AB, CF và DE đồng quy tại một điểm I.
b) Chứng minh tứ giác AEMO nội tiếp; hai tam giác MAB và OEF đồng dạng.