Đường tròn (O;R₁) và (O';R₂) tiếp xúc nhau tại P. Một cát tuyến qua P cắt (O;R₁) tại A và (O';R₂) tại B. Một cát tuyến khác cũng qua P cắt (O;R₁) tại C và (O';R₂) tại D. Chứng minh các tam giác PAC và PBD đồng dạng.

Cách giải 1: (Hình 1)

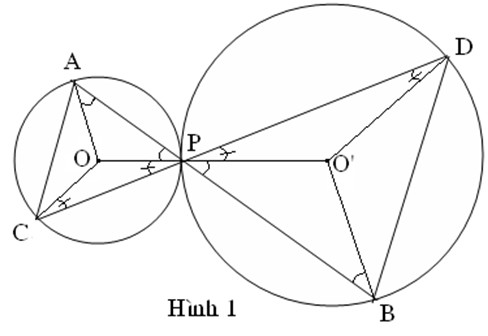
Ta có các tam giác OAP và tam giác O'BP là các tam giác cân tại O và O' Suy ra: $\widehat{OAP}=\widehat{OPA}$ và $\widehat{O\text{'}PB}=\widehat{O\text{'}BP}$ mà $\widehat{OPA}=\widehat{O\text{'}PB}$ (Hai góc đối đỉnh)
$\Rightarrow \widehat{OAP}=\widehat{PBO\text{'}}\Rightarrow$$△$OAP $~$$△$O'BP $\frac{PA}{PB}=\frac{PO}{PO\text{'}}=\frac{R_1}{R_2}$ (1)
Tương tự ta cũng có:
$\widehat{OCP}=\widehat{OPC}$ và $\widehat{O\text{'}PD}=\widehat{O\text{'}DP}$ mà $\widehat{OPC}=\widehat{O\text{'}PD}$ ( Hai góc đối đỉnh)
$\Rightarrow \widehat{OCP}=\widehat{PDO\text{'}}\Rightarrow$$△$OCP $~$ $△$O'DP $\Rightarrow \frac{PC}{PD}=\frac{PO}{PO\text{'}}=\frac{R_1}{R_2}$ (2)
Từ (1) và (2) ta có: $\frac{PA}{PB}=\frac{PC}{PD}=\frac{R_1}{R_2}$
Lại có $\widehat{CPA}=\widehat{BPD}$ Suy ra: 

Cách giải 2: (Hình 2)

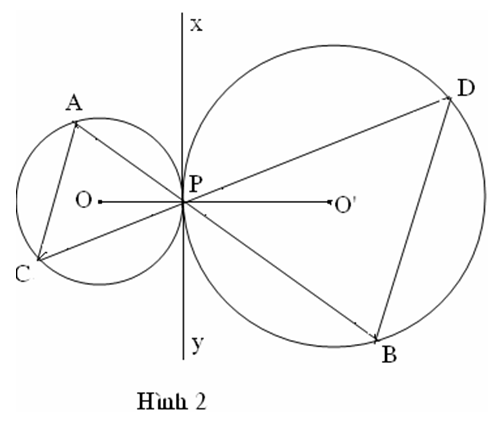
Kẻ tiếp tuyến chung xPy của hai đường tròn.
Ta có. $\widehat{CAP}=\widehat{CAy}=\widehat{xPD}=\widehat{PBD}$(Áp dụng tính chất về góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau)
Mặt khác $\widehat{APC}=\widehat{BPD}$ (hai góc đối đỉnh)
Suy ra : $△{\mathrm{PA}}_1{\mathrm{B}}_1~△{\mathrm{PA}}_2{\mathrm{B}}_2$