d, Gọi S là giao điểm của tia  BF và tiếp tuyến tại A của nửa đường tròn  Khi tứ giác  $AHIS$ nội tiếp được đường tròn. Chứng minh $EF\perp EK$

Cho nửa đường tròn tâm O đường kính AB và điểm E tùy ý trên nửa đường tròn đó (E khác A,B). Lấy điểm H thuộc đoạn EB (H khác E, B ). Tia AH cắt nửa đường tròn tại điểm thứ hai là F Kéo dài tia AE và BF cắt nhau tại I. Đường cao IH cắt nửa đường tròn tại P và cắt AB  tại K

a)    Chứng minh tứ giác IEHFnội tiếp được đường tròn

b,Tìm tất cả các giá trị của tham số  m để đường thẳng (d) cắt P tại hai điểm phân biệt có hoành độ $x_1,x_2$thỏa mãn điều kiện $x_1+x_2=x_1{x}_2$

Cho các số thực dương x,y thỏa mãn $x+y\le 3.$Tìm giá trị nhỏ nhất của biểu thức:

                  $P=\frac{1}{5xy}+\frac{5}{x+2y+5}.$

Rút gọn biểu thức $A=\frac{2}{3+\sqrt{7}}+\frac{\sqrt{28}}{2}-2$

Giải phương trình: ${\left(x^2-2x\right)}^2+{\left(x-1\right)}^2-13=0$

Giải hệ phương trình: $\left\{\begin{array}{l}x+3y=3\\ 4x-3y=-18\end{array}\right.$

  b, Chứng minh $\widehat{AIH}=\widehat{ABE}$

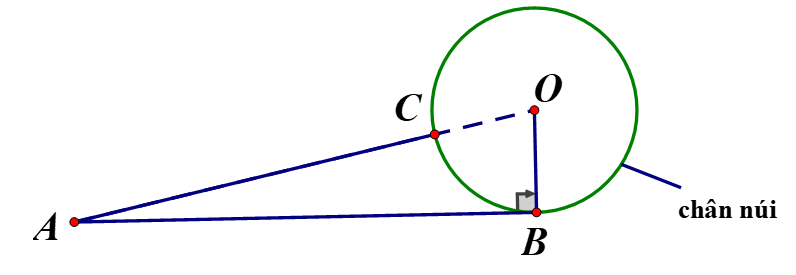
Có một vụ tai nạn ở vị trí B tại chân của một ngọn núi (chân núi có dạng đường tròn tâm O, bán kính 3km Và một trạm cứu hộ ở vị trí A (tham khảo hình vẽ). Do chưa biết đi đường nào dể đến vi trí tai nạn nhanh hơn nên đội cứu hộ quyết định diều hai xe cứu thương cùng xuất phát ở trạm cứu hộ đến vị trí tai nạn theo hai cách sau:

Xe thứ nhất: đi theo đường thẳng từ  A đến B, do đường xấu nên vận tốc trung bình của xe là 40km

Xe thứ hai: đi theo đường thẳng từ A đến C với vận tốc trung bình $60km/h$, rồi đi từ C đến B theo đường cung nhỏ CB ở chân núi với vận tốc trung bình $30km/h$(ba điểm A, O, C thẳng hàng và C ở chân núi). Biết đoạn đường AC dài 27km và $\widehat{AOB}={90}^0$

a, Tính độ dài quãng đường xe thứ nhất đi từ A đến B

Giải phương trình: $x^2-3x+2=0$

Cho parabo$\left(P\right):y=-2x^2$và đường thẳng $\left(d\right):y=x-m$ (với m là tham số)

    Vẽ parabol (P)