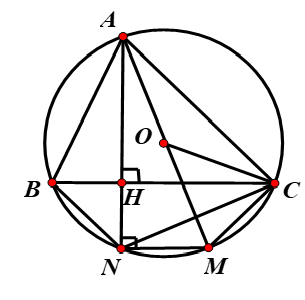
Cho tam giác ABC có ba góc nhọn, đường cao AH và nội tiếp đường tròn tâm O, đường kính AM.
a) Tính ;
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
a) Ta có (góc nội tiếp).
Cho đường tròn tâm O và một dây AB của đường tròn đó. Các tiếp tuyến vẽ từ A và B của đường tròn cắt nhau tại C. Gọi D là một điểm trên đường tròn có đường kính OC ( D khác A và B). CD cắt cung AB của đường tròn (O) tại E. (E nằm giữa C và D). Chứng minh rằng:
a) .
Cho (O) và hai dây MA và MB vuông góc với nhau. Gọi I, K lần lượt là điểm chính giữa của các cung nhỏ MA, MB. Gọi P là giao điểm của AK và BI.
a) CMR: A, O, B thẳng hàng.
Từ điểm M ở ngoài đường tròn (O), vẽ hai tiếp tuyến MA, MB và một cát tuyến MCD. Gọi I là giao điểm của AB và CD. Chứng minh rằng: .
Cho nửa đường tròn (O) đường kính CB, A thuộc nửa đường tròn sao cho AB < AC. Tiếp tuyến tại A cắt đường thẳng BC ở I. Kẻ AH vuông góc với BC. CMR:
a) AB là tia phân giác của góc IAH.
Cho tam giác ABC nội tiếp đường tròn (O). Tia phân giác góc A cắt BC tại D và cắt đường tròn tại điểm thứ hai là M. Kẻ tiếp tuyến AK với đường tròn (M, MB), K là tiếp điểm. Chứng minh rằng DK vuông góc với AM.
Cho tam giác ABC vuông tại A, đường cao AH. Vẽ (I) đường kính BH cắt AB ở M. Vẽ (K) đường kính CH cắt AC ở N.
a) Tứ giác AMHN là hình gì ? CM ?
Cho đường tròn (O) có các dây cung AB, BC, CA. Gọi M là điểm chính giữa của cung nhỏ AB. Vẽ dây MN song song với BC và gọi S là giao điểm của MN và AC. Chứng minh SM = SC và SN = SA.
Cho (O) đường kính AB; C chạy trên một nửa đường tròn. Vẽ đường tròn tâm I tiếp xúc với đường tròn (O) tại C, tiếp xúc với đường kính AB tại D. Đường tròn này cắt CA, CB lần lượt tại M và N.
a) CMR: 3 điểm M, I, N thẳng hàng .
Cho hình bình hành ABCD, góc A < 900. Đường tròn ngoại tiếp tam giác BCD cắt AC ở E. Chứng mình rằng BD là tiếp tuyến của đường tròn ngoại tiếp tam giác AEB.
c, Vẽ tiếp tuyến Ax của đường tròn ngoại tiếp tam giác ABC. CMR : Ax // MN.
Cho (O) và hai dây AB, CD bằng nhau và cắt nhau tại M. ( C thuộc cung nhỏ AB, B thuộc cung nhỏ CD).
a) CMR: cung AC = cung DB.
b, Tìm quỹ tích trung điểm M của CD khi cát tuyến CBD quay quanh B.
Trên nửa đường tròn (O) đường kính AB, lấy hai điểm M và N sao cho cung AM = cung MN = cung NB. Gọi P là giao điểm của AM và BN ; H là giao điểm của AN với BM. CMR :
a) Tứ giác AMNB là hình thang cân.
c) Gọi N là giao điểm AH với đường tròn (O). Tứ giác BCMN là hình gì? Vì sao?