Tìm tất cả các giá trị thực của tham số m sao cho phương trình có hai nghiệm thực?
A.
B.
C. m>1
D. đáp án khác
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Điều kiện: x≥ -1/2
Phương trình
Vì x= 0 không là nghiệm nên (*)
xét .
Ta có đạo hàm
Bảng biến thiên
Từ bảng biến thiên ta có để phương trình có hai nghiệm thì m ≥ 9/2.
Chọn D.
Cho hàm số: y = x3+2mx2+3(m-1)x+2 có đồ thị (C) . Đường thẳng d: y= - x+2 cắt đồ thị (C) tại ba điểm phân biệt A(0; -2); B và C. Với M(3;1) giá trị của tham số m để tam giác MBC có diện tích bằng là
Tìm tất cả các giá trị thực của tham số m sao cho hàm số đồng biến trên khoảng ?
Tìm tất cả các giá trị thực của tham số m sao cho phương trình có đúng 2 nghiệm dương?
Cho hàm số có đồ thị (C) . Tất cả các giá trị của tham số m để (C) cắt trục Ox tại ba điểm phân biệt có hoành độ x1; x2; x3 thỏa là
Cho hàm số có đồ thị (C) và đường thẳng d: y=x+m. Đường thẳng d cắt đồ thị (C) tại hai điểm A và B. Với C( -2; 5) , giá trị của tham số m để tam giác ABC đều là
Cho hàm số y= x4-(3m+4)x2+m2 có đồ thị là (C). Có mấy giá trị nguyên của m để đồ thị (C) cắt trục hoành tại bốn điểm phân biệt có hoành độ lập thành một cấp số cộng.
Tìm tất cả các giá trị thực của tham số m sao cho mọi nghiệm của bất phương trình: x2- 3x+ 2≤ 0 cũng là nghiệm của bất phương trình mx2 + (m + 1) x + m + 2≥0?
Bất phương trình có tập nghiệm là [a; b]. Hỏi tổng a2+ b2 có giá trị là bao nhiêu?
Tìm tất cả các giá trị của tham số m để đồ thị hàm số y = x3-3( m+1) x2+ 12mx-3m+ 4 ( C) có hai điểm cực trị là A và B sao cho hai điểm này cùng với điểm C(-1; -9/2) lập thành tam giác nhận gốc tọa độ làm trọng tâm.
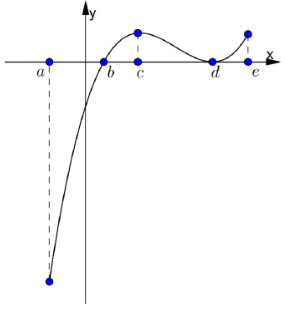
Cho hàm số y= f(x) xác định và liên tục trên [ a; e] và có đồ thị hàm số y= f’ (x) như hình vẽ bên. Biết rằng f(a) + f( c)) = f( b) + f( d) . Tìm giá trị lớn nhất và nhỏ nhất của hàm số y= f( x) trên [ a; e]?
Cho hàm số y= x3-3x2-m-1 có đồ thị (C) . Giá trị của tham số m để đồ thị (C) cắt trục hoành tại ba điểm phân biệt lập thành cấp số cộng là
Tìm tất cả các giá trị thực của tham số sao cho bất phương trình: nghiệm đúng mọi x≥ 1 ?
Tìm tất cả các giá trị thực của tham số m sao cho phương trình có hai nghiệm thực?
Cho hàm số y= x4- 2( 1-m2) x2+ m+1. Tồn tại giác trị của m để hàm số có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số lập thành tam giác có diện tích lớn nhất . Khi đó khẳng định nào đúng?