Cho tứ diện đều có cạnh bằng 3. M là một điểm thuộc miền trong của khối tứ diện tương ứng. Tính giá trị lớn nhất của tích các khoảng cách từ điểm M đến bốn mặt của tứ diện đã cho.
A. 36
B. 9/64
C.
D.
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Chọn B
Gọi r₁, r₂, r₃, r₄ là khoảng cánh từ điểm M đến bốn mặt của tứ diện.
Gọi S là diện tích một mặt của tứ diện
Đường cao của tứ diện là .
Thể tích của tứ diện là .
Mặt khác, ta có:
Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy. Gọi M là trung điểm của CD. Biết khoảng cách giữa hai đường thẳng BC và SM bằng . Tính thể tích của khối chóp đã cho theo a.
Cho lăng trụ tam giác đều ABC. A'B'C' có tất cả các cạnh đều bằng a. Khoảng cách giữa hai đường thẳng BC và AB' bằng:
Cho khối lăng trụ tam giác đều ABC. A'B'C' có cạnh đáy là a và khoảng cách từ A đến mặt phẳng (A'BC) bằng a/2. Thể tích của khối lăng trụ bằng:
Cho hình chóp S. ABC có SA, SB, SC đôi một vuông góc với nhau và SA=SB=SC=a. Sin của góc giữa đường thẳng SC và mặt phẳng (ABC) bằng:
Cho hình chóp S. ABC có đáy ABC là tam giác đều cạnh bằng a, tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy, SC hợp với đáy một góc 300, M là trung điểm của AC. Tính thể tích khối chóp S. BCM.
Cho hình chóp tứ giác đều S. ABCD, M là trung điểm của SC. Mặt phẳng (P) qua AM và song song với BD cắt SB, SD tại N, K. Tính tỉ số thể tích của khối S. ANMK và khối chóp S.ABCD.
Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a, SA = a và SA vuông góc với đáy. Gọi M là trung điểm SB, N thuộc cạnh SD sao cho SN = 2ND. Tính thể tích V của khối tứ diện ACMN.
Cho hình chóp S.ABC có cạnh bên SA vuông góc với đáy, AB = a, BC = , SC=2a và ![]() . Tính bán kính R của mặt cầu ngoại tiếp tứ diện S.ABC
. Tính bán kính R của mặt cầu ngoại tiếp tứ diện S.ABC
Cho khối hộp ABCD. A'B'C'D' có đáy là hình chữ nhật với AB = ; AD = . Hai mặt bên (ABB'A') và (ADD'A') cùng tạo với đáy góc 450, cạnh bên của hình hộp bằng 1 (hình vẽ). Thể tích khối hộp là:

Cho tứ diện OABC biết OA, OB, OC đôi một vuông góc với nhau, biết OA=3, OB=4 và thể tích khối tứ diện OABC bằng 6. Khi đó khoảng cách từ O đến mặt phẳng (ABC) bằng:
Cho hình chóp S. ABC, có AB=5 (cm), BC=6 (cm), AC=7 (cm). Các mặt bên tạo với đáy 1 góc 600. Thể tích của khối chóp bằng:
Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với đáy, biết SC = . Gọi M, N, P, Q lần lượt là trung điểm các cạnh SB, SD, CD, BC. Tính thể tích khối chóp AMNPQ
Cho khối lăng trụ tam giác ABC. A'B'C'. Gọi M, N lần lượt là trung điểm của BB' và CC'. Mặt phẳng (AMN) chia khối lăng trụ thành hai phần. Gọi V₁ là thể tích của khối đa diện chứa đỉnh B' và V₂ là thể tích khối đa diện còn lại. Tính tỉ số V₁/V₂.
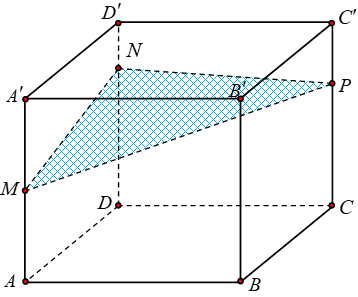
Cho khối hộp chữ nhật ABCD. A'B'C'D' có thể tích bằng 2110. Biết (MNP), DN=3ND', CP=2C'P như hình vẽ. Mặt phẳng (MNP) chia khối hộp đã cho thành hai khối đa diện. Thể tích khối đa diện nhỏ hơn bằng:
Cho hình chóp tứ giác đều S. ABCD. Mặt phẳng (P) chứa đường thẳng AC và vuông góc với mặt phẳng (SCD), cắt đường thẳng SD tại E. Gọi V và V₁ lần lượt là thể tích các khối chóp S.ABCD và D.ACE. Tính số đo góc tạo bởi mặt bên và mặt đáy của hình chóp S.ABCD biết V = 5