Có bao nhiêu số phức z thỏa mãn |z + 3i| = và là số thuần ảo ?
A. vô số
B. 2
C. 0
D. 1
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Đáp án D
Đặt ![]()
![]()
![]()
Ta có: ![]()
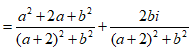 là số thuần ảo thì
là số thuần ảo thì
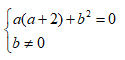
Khi đó ta có hệ:
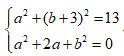
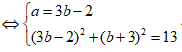
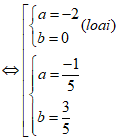
Vậy chỉ có 1 số phức z thỏa mãn.
Có bao nhiêu số phức z thỏa mãn |z-3i| = 5 và là số thuần ảo ?
Kí hiệu là hai nghiệm phức của phương trình + 4 = 0. Gọi M,N lần lượt là các điểm biểu diễn của trên mặt phẳng tọa độ.Tính T = OM+ON với O là gốc tọa độ.
Cho số phức z = 1 - 2i . Điểm nào dưới đây là điểm biểu diễn của số phức w = iz trên mặt phẳng tọa độ ?
Cho số phức z thỏa mãn |z| = 5 và |z + 3| = |z + 3 - 10i| .Tính số phức w=z-4+3i
Cho số phức z thỏa mãn |z + 3| = 5 và |z - 2i| = |z - 2 - 2i|. Tính |z|
Kí hiệu là hai nghiệm phức của phương trình - z + 1 = 0. Tính P = ||+||
Cho hai số phức = 1-3i và = -2-5i . Tìm phần ảo b của số phức z = -
Cho số phức z = a + bi, (a, b ) thỏa mãn z + 1 + 3i - |z|i = 0. Tính S = a + 3b
Kí hiệu là hai nghiệm phức của phương trình - z + 6 = 0 . Tính P =