Cho số phức z có phần ảo âm, gọi w = 2z + |z-|i. Khi đó khẳng định nào sau đây về w là đúng?
A. w là số thực
B. w có phần thực bằng 0
C. w có phần ảo âm
D. w có phần ảo dương
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Đáp án A
Đặt ![]() vì z có phần ảo âm suy ra y < 0. Khi đó
vì z có phần ảo âm suy ra y < 0. Khi đó
![]()
![]()
![]()
Vậy w là một số thực.
Trong mặt phẳng tọa độ Oxy, tìm tập hợp điểm biểu diễn các số phức z thỏa mãn |z-i| = |(1+i)z|
Gọi số phức z = a + bi(a,b) thỏa mãn |z-1| = 1 và (1+i)(-1) có phần thực bằng 1 đồng thời z không là số thực. Khi đó a.b bằng
Cho hai số phức , thỏa mãn || = || = |-| = 1. Tính giá trị của biểu thức P =
Cho số phức thỏa mãn |z| 1. Đặt A = . Mệnh đề nào sau đây đúng?
Gọi , là hai nghiệm phức của phương trình + 2z + 10 = 0. Tính giá trị của biểu thức A =
Trong mặt phẳng phức, gọi M là điểm biểu diễn số phức với z = a + bi(a,b). Chọn kết luận đúng.
Cho số phức z thỏa mãn (3-4i)z - = 8. Trên mặt phẳng tọa độ, khoảng cách từ gốc tọa độ đến điểm biểu diễn số phức z thuộc tập nào?
Gọi là hai nghiệm của phương trình - 2z + 2 = 0. Tính giá trị của biểu thức P =
Cho A, B, C là những điểm biểu diễn các số phức thỏa mãn + i = 0. Tìm phát biểu sai?
Tập hợp các điểm biểu diễn số phức z thỏa mãn 2|z-1| = |z + +2| trên mặt phẳng tọa độ là một
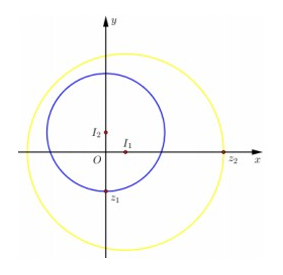
Gọi T là tập hợp các số phức z thỏa mãn |z-i|3 và |z-i|5. Gọi lần lượt là các số phức có môđun nhỏ nhất và lớn nhất. Tìm số phức
Kí hiệu là nghiệm phức có phần thực âm và phần ảo dương của phương trình + 2z + 10 = 0. Trên mặt phẳng tọa độ, điểm nào dưới đây là điểm biểu diễn số phức w = ?