Kết quả của phép tính: P = 1 + i + ..... +
A. P = 0
B. P = 1
C. P = 1 + i
D. P = 2i
Giải bởi qa.haylamdo.com
Đáp án C
Em thấy trong biểu thức P gồm bao nhiêu số hạng và các số hạng có quan hệ gì?
P có 2018 số hạng. Nếu em tính riêng mỗi số hạng ik với k = 1,2,...., 2016,2017 thì việc cộng các kết quả đó cũng không đơn giản chút nào.
Kể từ số hạng thứ hai, số hạng sau gấp số hạng đứng ngay trước nó là i. Vậy nên P là tổng của 2018 số hạng đầu của một cấp số nhân, với số hạng đầu là = 1 và công bội q = i. Sử dụng công thức tính tổng của n số hạng đầu của cấp số nhân với số hạng dầu và công bội q:
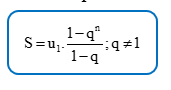
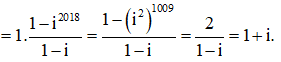
Gọi là hai nghiệm phức của phương trình - 2z + 2 = 0. Khi đó giá trị biểu thức A = bằng:
Gọi z1, z2 là hai nghiệm của phương trình + z + 1 = 0. Tính giá trị của biểu thức ?
Cho số phức z thay đổi hoàn toàn thỏa mãn: |z-i| = |z-1+2i|. Tập hợp các điểm trên mặt phẳng tọa độ biểu diễn số phức w thỏa mãn: w = (2-i)z+1 là một đường thẳng. Viết phương trình đường thẳng đó.
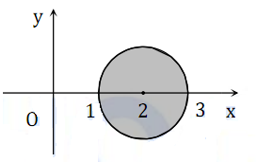
Biết các số phức z có tập hợp điểm trên mặt phẳng tọa độ là hình tròn tô đậm như hình vẽ. Modul lớn nhất của số phức z là:
Số phức nào dưới đây có điểm biểu diễn trên mặt phẳng tọa độ là điểm M như hình bên?
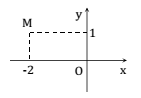
Trong mặt phẳng phức cho điểm . Trong các khẳng định sau, khẳng định nào sai?
Cho số phức z thỏa mãn điều kiện (z+2)(1+2i) = 5. Tìm phần ảo của số phức w =
Tìm tổng các giá trị của m để hai phương trình + mz + 2 = 0 và - + 2z + m có ít nhất một nghiệm phức chung.
Gọi z1, z2, z3 và z4 là bốn nghiệm phức của phương trình - 12 = 0. Tính tổng T = |z1| + |z2| + |z3| + |z4|
Cho số phức z thỏa mãn |z+i| = 1. Biết rằng tập hợp các điểm biểu diễn các số phức w = z - 2i là một đường tròn. Tâm của đường tròn đó là:
Phương trình: - 6(z + 3 - i) + 13 = 0 có 2 nghiệm phân biệt. Khẳng định nào sau đây là đúng?
Cho số phức z thỏa mãn |z+2i+3| = |-i|. Tìm giá trị nhỏ nhất của |z|.
