Miền hình phẳng trong hình vẽ được giới hạn bởi đường cong , trục hoành, trục tung và đường thẳng x = 2. Biết thì diện tích hình phẳng đó đạt giá trị nhỏ nhất. Giá trị gần giá trị nào nhất trong các giá trị sau?
A. 0.
B. 1.
C. 4.
D. -3.
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Đáp án A.
Cho Parapol (P): và đường thẳng (d): . Tìm m để diện tích hình phẳng giới hạn bởi (P) và (d) đạt giá trị nhỏ nhất?
Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục hoành, đường thẳng x = a, x = b ( như hình bên). Biết và . Hỏi S bằng bao nhiêu?
Cho (H) là hình phẳng giới hạn bởi cung tròn có bán kính R=2, đường cong và trục hoành ( miền tô đậm như hình vẽ).
.jpg)
Tính thể tích V của khối tạo thành khi cho hình (H) quay quanh trục Ox.
Cho hình phẳng (H) giới hạn bởi các đường y = tanx, y = 0; x = 0, . Khi đó thể tích V của khối tròn xoay tạo ra khi quay (H) quay quanh trục Ox bằng bao nhiêu?
Miền hình phẳng trong hình vẽ được giới hạn bởi đường cong và . Biết 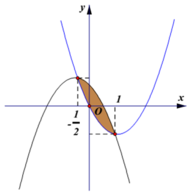
Khi đó diện tích hình phẳng được tô trên hình vẽ là
Cho tích phân . Biết kết quả với . Khi đó a-b+c bằng bao nhiêu?
Cho hình phẳng (H) giới hạn bởi đồ thị hàm số , trục hoành, trục tung và đường thẳng x=1 thì diện tích hình (H) là:
Nếu F(x) là một nguyên hàm của hàm số và đồ thị y = F(x) đi qua điểm thì F(x) là
Cho hình phẳng (H) giới hạn bởi các đường , và hai trục tọa độ. Đường thẳng x = k chia (H) thành hai phần có diện tích S1, S2 như hình vẽ bên. Để S1 = 6S2 thì . Hỏi gần giá trị nào nhất trong các giá trị sau?
Cho hình phẳng (H) giới hạn bởi các đường y=sinx, , hai trục tọa độ. Thể tích V của khối tròn xoay khi quay (H) quanh trục Ox là
Cho hình phẳng (H) giới hạn bới các đường , và . Diện tích S của hình phẳng (H) là