Thiết diện qua trục của một hình nón là một tam giác vuông có diện tích bằng . Diện tích toàn phần của hình nón bằng
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Đáp án C.
Trên bức tường cần trang trí một hình phẳng dạng parabol đỉnh S như hình vẽ. Biết , O là trung điểm AB. Parabol trên được chia thành ba phần để sơn ba màu khác nhau với mức chi phí: Phần kẻ sọc 140000 đồng / , phần giữa là hình quạt tâm O, bán kính 2m được tô đậm 150000 đồng / , phần còn lại 160000 đồng / . Tổng chi phí để sơn ba phần gần nhất với số nào sau đây?
Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây?
Cho hình phẳng (H) giới hạn bởi đồ thị hàm số và trục hoành. Thể tích vật thể tròn xoay khi quay (H) quanh trục hoành bằng
Cho hình vuông OABC có cạnh bằng 4 được chia thành hai phần bởi đường parabol (P) có đỉnh tại O. Gọi S là hình phẳng không bị gạch (như hình vẽ).
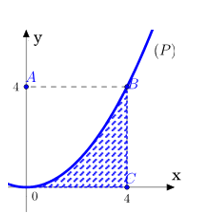
Tính thể tích V của khối tròn xoay khi cho phần S quay quanh trục Ox
Một khuôn viên dạng nửa hình tròn, trên đó người ta thiết kế phần trồng hoa hồng có dạng một hình parabol có đỉnh trùng với tâm hình tròn và có trục đối xứng vuông góc với đường kính của nửa đường tròn, hai đầu mút của parabol nằm trên nửa đường tròn cách nhau một khoảng 4 mét (phần tô đậm). Phần còn lại của khuôn viên (phần không tô màu) dùng để trồng hoa cúc. Biết các kích thước cho như hình vẽ. Chi phí trồng hoa hồng và hoa cúc lần lượt là 120.000 đồng và 80.000 đồng.
Hỏi chi phí trồng hoa khuôn viên đó gần nhất với số tiền nào dưới đây (làm tròn đến nghìn đồng)?
Cho hàm số liên tục trên đoạn [a;b], có đồ thị tạo với trục hoành một hình phẳng gồm ba phần có diện tích S1,S2,S3 như hình vẽ.
Tích phân bằng